50 bài tập định nghĩa đạo hàmLàm bàiQuảng cáo
Câu hỏi 1 : Phát biểu nào trong các phát biểu sau là đúng?
Đáp án: D Phương pháp giải: Phương pháp: Định nghĩa đạo hàm: Nếu hàm số \(f\left( x \right)\) xác định tại \({x_0}\) và tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) thì hàm số \(f\left( x \right)\) có đạo hàm tại \({x_0}\). Định nghĩa hàm số liên tục tại một điểm: Nếu hàm số \(f\left( x \right)\) xác định tại \({x_0}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) thì hàm số liên tục tại \({x_0}\). Lời giải chi tiết: Cách giải: Dựa vào định nghĩa đạo hàm, ta có kết quả: Nếu hàm số \(y = f\left( x \right)\) có đạo hàm tại \({x_0}\) thì tồn tại giới hạn \(L = \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). Do đó \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) vì nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \pm \infty \) Do đó hàm số liên tục tại điểm \(x = {x_0}\). Chọn đáp án D Câu hỏi 2 : Cho hàm số \(y=f\left( x \right)=\left\{ \begin{align}& {{x}^{2}}+1,\,\,x\ge 1 \\& 2x,\,\,\,\,\,\,\,\,x<1.\, \\\end{align} \right.\) Mệnh đề sai là
Đáp án: B Phương pháp giải: Phương pháp. Sử dụng định nghĩa, công thức đạo hàm cơ bản để tính trực tiếp đạo hàm và kết luận. Lời giải chi tiết: Lời giải chi tiết. Ta có \(x>1\) thì \(f\left( x \right)={{x}^{2}}+1\) nên \(f'\left( x \right)=2x\Rightarrow f'\left( 2 \right)=2.2=4.\) Đáp án D đúng. Tương tự ta có \(f'\left( 0 \right)=2\) đáp án C đúng. Ta kiểm tra xem \(f\) có đạo hàm tại \({{x}_{0}}=1\) hay không? Ta có \(\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{\left( {{x}^{2}}+1 \right)-2}{x-1}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{{{x}^{2}}-1}{x-1}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\left( x+1 \right)=2.\) Tương tự ta có \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{2x-2}{x-1}=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{2\left( x-1 \right)}{x-1}=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,2=2.\) Như vậy \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=2.\) Do đó \(f'\left( 1 \right)=2.\) Đáp án A đúng. Chọn đáp án B. Câu hỏi 3 : Cho hàm số \(f\left( x \right)=\sqrt{x+1}\). Tính đạo hàm của hàm số tại điểm \({{x}_{0}}=1\)
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: TXĐ: \(D=\left[ -1;+\infty \right)\) \(f'\left( 1 \right)=\underset{x\to 1}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{\sqrt{x+1}-\sqrt{2}}{x-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{x+1-2}{\left( x-1 \right)\left( \sqrt{x+1}+\sqrt{2} \right)}=\underset{x\to 1}{\mathop{\lim }}\,\frac{1}{\sqrt{x+1}+\sqrt{2}}=\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}\) Chọn A. Câu hỏi 4 : Khi tính đạo hàm của hàm số \(f\left( x \right)={{x}^{2}}+5x-3\) tại điểm \({{x}_{0}}=2\), một học sinh đã tính theo các bước sau: Bước 1: \(f\left( x \right)-f\left( 2 \right)=f\left( x \right)-11\) Bước 2: \(\frac{f\left( x \right)-f\left( 2 \right)}{x-2}=\frac{{{x}^{2}}+5x-3-11}{x-2}=\frac{\left( x-2 \right)\left( x+7 \right)}{x-2}=x+7\) Bước 3: \(\underset{x\to 2}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 2 \right)}{x-2}=\underset{x\to 2}{\mathop{\lim }}\,\left( x+7 \right)=9\Rightarrow f'\left( 2 \right)=9\) Tính toán trên nếu sai thì sai ở bước nào?
Đáp án: D Phương pháp giải: Xét tính đúng sai ở từng bước. Lời giải chi tiết: Bài giải trên hoàn toàn đúng. Chọn D. Câu hỏi 5 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3 - \sqrt {4 - x} \,\,\,khi\,\,x \ne 0\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Khi đó \(f'\left( 0 \right)\) là kết quả nào sau đây?
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: \(f'\left( 0 \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}=\underset{x\to 0}{\mathop{\lim }}\,\frac{3-\sqrt{4-x}-1}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{2-\sqrt{4-x}}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{4-4+x}{x\left( 2+\sqrt{4-x} \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{1}{2+\sqrt{4-x}}=\frac{1}{4}\) Chọn A. Câu hỏi 6 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt x \,\,\,khi\,\,x > 1\\{x^2}\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\). Tính \(f'\left( 1 \right)\) ?
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{\sqrt x + 1}} = \frac{1}{2}\\\mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x + 1} \right) = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} \ne \mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\end{array}\) Vậy không tồn tại đạo hàm của hàm số tại x = 1. Chọn D. Câu hỏi 7 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt x }}{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Xét hai mệnh đề sau: (I) \(f'\left( 0 \right)=1\) (II) Hàm số không có đạo hàm tại \({{x}_{0}}=0\) Mệnh đề nào đúng?
Đáp án: B Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: Ta có: \(\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{x}}{{{x}^{2}}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{1}{x\sqrt{x}}=+\infty \Rightarrow \) Hàm số không có đạo hàm tại x = 0. Chọn B. Câu hỏi 8 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\\\frac{{{x^3} + 2{x^2} - 7x + 4}}{{x - 1}}\,\, \, \, khi\,\,x < 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x + 3 - 5}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 2}}{{x - 1}} = 2\\\mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\frac{{{x^3} + 2{x^2} - 7x + 4}}{{x - 1}} - 5}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^3} + 2{x^2} - 12x + 9}}{({x - 1})^2} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left( {x - 1} \right)\left( {{x^2} + 3x - 9} \right)}}{({x - 1})^2}\\ = \mathop {\lim }\limits_{x \to {1^ - }} {{ {{x^2} + 3x - 9} }\over{x-1} }= +\infty.\\ \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} \ne \mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\end{array}\) Vậy hàm số không tồn tại đạo hàm tại x = 1. Chọn D. Câu hỏi 9 : Cho hàm số \(y=f\left( x \right)\) xác định: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 1} - 1}}{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại) Lời giải chi tiết: \(f'\left( 0 \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{\sqrt{{{x}^{2}}+1}-1}{x}}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}+1}-1}{{{x}^{2}}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}+1-1}{{{x}^{2}}\left( \sqrt{{{x}^{2}}+1}+1 \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\sqrt{{{x}^{2}}+1}+1}=\frac{1}{2}\) Chọn A. Câu hỏi 10 : Xét hai mệnh đề: (I) f(x) có đạo hàm tại x0 thì f(x) liên tục tại x0 (II) f(x) liên tục tại x0 thì f(x) có đạo hàm tại x0 Mệnh đề nào đúng?
Đáp án: A Phương pháp giải: Suy luận từ công thức tính đạo hàm của hàm số tại một điểm bằng định nghĩa. Lời giải chi tiết: (I) hiển nhiên đúng. (II) sai. Ví dụ: Xét hàm số \(f\left( x \right)=\left| x \right|\) ta có \(\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,=\left| {{x}_{0}} \right|=f\left( {{x}_{0}} \right)\Rightarrow \) Hàm số liên tục tại trên R. Tuy nhiên hàm số không có đạo hàm tại x = 0 \(\begin{array}{l}f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{\left| x \right| - 0}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{\left| x \right|}}{x}\\\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right|}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{\left| x \right|}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{x} = - 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right|}}{x} \ne \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\left| x \right|}}{x}\end{array}\) Không tồn tại đạo hàm của hàm số tại x = 0. Chọn A. Câu hỏi 11 : Xét ba hàm số: \(\left( I \right):f\left( x \right)=\left| x \right|x,\,\,\left( II \right):g\left( x \right)=\sqrt{x}\) . Hàm số có đạo hàm tại x = 0 là:
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} x = 0\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - {x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x} \right) = 0\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = 0 \Rightarrow \) Hàm số \(y=f\left( x \right)\) có đạo hàm tại x = 0. \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{g\left( x \right)-g\left( 0 \right)}{x-0}=\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{\sqrt{x}}{x}=+\infty \Rightarrow \) Hàm số \(y=g\left( x \right)\) không có đạo hàm tại x = 0. Chọn A. Câu hỏi 12 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt[3]{{4{x^2} + 8}} - \sqrt {8{x^2} + 4} }}{x^2}\,\,\,khi\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:
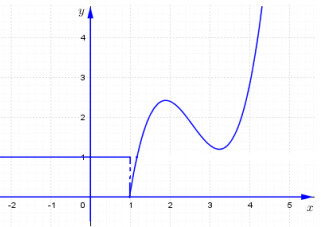
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: Để hàm số có đạo hàm tại x = 0, trước hết hàm số phải liên tục tại x = 0. Ta có : \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{4{x^2} + 8}} - \sqrt {8{x^2} + 4} }}{{{x^2}}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{4{x^2} + 8}} - 2}}{{{x^2}}} - \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {8{x^2} + 4} - 2}}{{{x^2}}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{4{x^2}}}{{{x^2}\left( {{{\sqrt[3]{{4{x^2} + 8}}}^2} + 2\sqrt[3]{{4{x^2} + 8}} + 4} \right)}} - \mathop {\lim }\limits_{x \to 0} \frac{{8{x^2}}}{{{x^2}\left( {\sqrt {8{x^2} + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{4}{{{{\sqrt[3]{{4{x^2} + 8}}}^2} + 2\sqrt[3]{{4{x^2} + 8}} + 4}} - \mathop {\lim }\limits_{x \to 0} \frac{8}{{\sqrt {8{x^2} + 4} + 2}} = \frac{1}{3} - 2 = - \frac{5}{3}\end{array}\) \(f\left( 0 \right) = 0\) \( \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) \ne f\left( 0 \right)\), do đó hàm số không liên tục tại \(x = 0\). Vậy hàm số không có đạo hàm tại \(x = 0\). Chọn D. Câu hỏi 13 : Cho đồ thị hàm số \(y=f\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây sai?
Đáp án: B Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy \(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=1,\,\,\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=0\Rightarrow \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)\ne \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)\Rightarrow \) Không tồn tại \(\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)\), hàm số không liên tục tại x = 1. Vậy hàm số không có tại hàm tại x = 1 Chọn B. Câu hỏi 14 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 4{x^2} + 3x}}{{{x^2} - 3x + 2}}\,\,\,khi\,\,x \ne 1\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: Ta có: \(f'\left( 1 \right)=\underset{x\to 1}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{\frac{{{x}^{3}}-4{{x}^{2}}+3x}{{{x}^{2}}-3x+2}}{x-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{x\left( x-3 \right)\left( x-1 \right)}{{{\left( x-1 \right)}^{2}}\left( x-2 \right)}=\underset{x\to 1}{\mathop{\lim }}\,\frac{x\left( x-3 \right)}{\left( x-1 \right)\left( x-2 \right)}=-\infty \) Vậy hàm số không có đạo hàm tại x = 1. Chọn D. Câu hỏi 15 : Cho hàm số \(f\left( x \right)=\frac{{{x}^{2}}+\left| x+1 \right|}{x}\). Tính đạo hàm của hàm số tại \({{x}_{0}}=-1\).
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: \(f'\left( -1 \right)=\underset{x\to \left( -1 \right)}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( -1 \right)}{x+1}\) Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{\frac{{{x^2} + x + 1}}{x} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 2x + 1}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{x + 1}}{x} = 0\\\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{\frac{{{x^2} - x - 1}}{x} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{{x^2} - 1}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{x - 1}}{x} = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} \ne \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\end{array}\) Do đó không tồn tại \(\underset{x\to \left( -1 \right)}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( -1 \right)}{x+1}\), vậy không tồn tại đạo hàm của hàm số tại \({{x}_{0}}=-1\). Chọn D. Câu hỏi 16 : Xét hai câu sau: (1) Hàm số \(y=\frac{\left| x \right|}{x+1}\) liên tục tại x = 0. (2) Hàm số \(y=\frac{\left| x \right|}{x+1}\) có đạo hàm tại x = 0. Trong 2 câu trên:
Đáp án: B Phương pháp giải: +) Hàm số liên tục tại \(x={{x}_{0}}\Leftrightarrow \underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f\left( x \right)=f\left( 0 \right)\) +) Hàm số có đạo hàm tại \(x={{x}_{0}}\Leftrightarrow f'\left( {{x}_{0}} \right)=\underset{x\to x_{0}^{+}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}=\underset{x\to x_{0}^{-}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) Lời giải chi tiết: Ta có: \(y = \frac{{\left| x \right|}}{{x + 1}} = \left\{ \begin{array}{l}\frac{x}{{x + 1}}\,\,\,khi\,x \ge 0\\\frac{{ - x}}{{x + 1}}\,\,\,khi\,\,x < 0\end{array} \right.\) Ta có \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{{x + 1}} = 0 = f\left( 0 \right)\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{{x + 1}} = 0\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( 0 \right) = 0 \Rightarrow \) Hàm số liên tục tại x = 0. \(f'\left( 0 \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\frac{x}{{x + 1}} - 0}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{x + 1}} = 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\frac{{ - x}}{{x + 1}} - 0}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - 1}}{{x + 1}} = - 1\end{array} \right. \Rightarrow x = {x_0} \Rightarrow \mathop {\lim }\limits_{x \to x_0^ + } \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \ne \mathop {\lim }\limits_{x \to x_0^ - } \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \Rightarrow \) Hàm số không tồn tại đạo hàm tại x = 0. Chọn B. Câu hỏi 17 : Tìm a để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\,\,khi\,\,x \ne 1\\a\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\) có đạo hàm tại x = 1.
Đáp án: B Phương pháp giải: +) Để hàm số có đạo hàm tại x = 1 thì hàm số phải liên tục tại x = 1. +) Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại). Lời giải chi tiết: Để hàm số có đạo hàm của hàm số tại điểm x = 1 thì trước hết hàm số phải liên tục tại x = 1, tức là \(\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)=f\left( 1 \right)\Leftrightarrow \underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{2}}-1}{x+1}=a\Leftrightarrow \underset{x\to 1}{\mathop{\lim }}\,\left( x+1 \right)=a\Leftrightarrow 2=a\) Khi đó hàm số có dạng: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\,\,khi\,\,x \ne 1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\) \(\Rightarrow f'\left( 1 \right)=\underset{x\to 1}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to 1}{\mathop{\lim }}\,\frac{\frac{{{x}^{2}}-1}{x-1}-2}{x-1}\underset{x\to 1}{\mathop{\lim }}\,\frac{\left( x+1 \right)\left( x-1 \right)-2\left( x-1 \right)}{{{\left( x-1 \right)}^{2}}}=\underset{x\to 1}{\mathop{\lim }}\,\frac{x+1-2}{x-1}=1\) Vậy a = 2. Chọn B. Câu hỏi 18 : Tìm a, b để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} + 1}}{{x + 1}}\,\,khi\,\,x \ge 0\\ax + b\,\,khi\,\,x < 0\end{array} \right.\) có đạo hàm tại điểm x = 0.
Đáp án: D Phương pháp giải: +) Trước hết hàm số liên tục tại x = 0. +) Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\Leftrightarrow f'\left( {{x}_{0}} \right)=\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}\) Lời giải chi tiết: Trước tiên hàm số phải liên tục tại x = 0. Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2} + 1}}{{x + 1}} = 1\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {ax + b} \right) = b = f\left( 0 \right)\end{array}\) Để hàm số liên tục tại x = 0 thì \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( 0 \right)\Leftrightarrow b=1\) Khi đó ta có \(f'\left( 0 \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}\) Ta có \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\frac{{{x^2} + 1}}{{x + 1}} - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2} - x}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{x - 1}}{{x + 1}} = - 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left( {ax + 1} \right) - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} a = a\end{array}\) Để hàm số có đạo hàm tại x = 0 thì \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x}\Leftrightarrow a=-1\) Vậy \(a=-1,b=1\). Chọn D. Câu hỏi 19 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx\,\,khi\,\,x \ge 1\\2x - 1\,\,\,\,\,\,\,khi\,\,x < 1\end{array} \right.\). Tìm a, b để hàm số có đạo hàm tại x = 1.
Đáp án: C Phương pháp giải: +) Tìm điều kiện để hàm số liên tục tại x = 1: \(\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( 1 \right)\) +) Tìm điều kiện để hàm số có đạo hàm tại x = 1: \(f'\left( 1 \right)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}\) Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {a{x^2} + bx} \right) = a + b = f\left( 1 \right)\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {2x - 1} \right) = 1\end{array}\) Để hàm số liên tục tại x = 1 thì \(\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( 1 \right)\Leftrightarrow a+b=1\,\,\,\left( 1 \right)\) Khi đó ta có: \(f'\left( 1 \right)=\underset{x\to 1}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}\) \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{a{x^2} + bx - \left( {a + b} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{a\left( {{x^2} - 1} \right) + b\left( {x - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \left[ {a\left( {x + 1} \right) + b} \right] = 2a + b\\\mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x - 1 - \left( {a + b} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{2x - 2}}{{x - 1}} = 2\end{array}\) Để hàm số có đạo hàm tại x = 1 thì \(f'\left( 1 \right)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 1 \right)}{x-1}\Leftrightarrow 2a+b=2\,\,\,\left( 2 \right)\) Từ (1) và (2) ta có hệ: \(\left\{ \begin{array}{l}a + b = 1\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\) Chọn C. Câu hỏi 20 : Với hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x\sin \frac{\pi }{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Để tìm đạo hàm \(f'\left( 0 \right)\) một học sinh lập luận qua các bước sau: Bước 1: \(\left| f\left( x \right) \right|=\left| x \right|\left| \sin \frac{\pi }{x} \right|\le \left| x \right|\) Bước 2: Khi \(x\to 0\) thì \(\left| x \right|\to 0\) nên \(\left| f\left( x \right) \right|\to 0\Rightarrow f\left( x \right)\to 0\) Bước 3: Do \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( 0 \right)=0\) nên hàm số liên tục tại x = 0. Bước 4: Từ f(x) liên tục tại \(x=0\Rightarrow f\left( x \right)\) có đạo hàm tại x = 0. Lập luận trên nếu sai thì bắt đầu từ bước nào?
Đáp án: D Phương pháp giải: Để hàm số có đạo hàm tại x0 thì hàm số liên tục tại x0, điều ngược lại chưa chắc đúng. Lời giải chi tiết: Một hàm số liên tục tại x0 chưa chắc có đạo hàm tại điểm đó, hơn nữa \(\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}=\underset{x\to 0}{\mathop{\lim }}\,\frac{x\sin \frac{\pi }{x}-0}{x}=\underset{x\to 0}{\mathop{\lim }}\,\sin \frac{\pi }{x}=+\infty \Rightarrow \) Hàm số không có đạo hàm tại x = 0. Lập luận trên sai từ bước 4. Chọn D. Câu hỏi 21 : Cho hàm số \(f\left( x \right)=x\left( x-1 \right)\left( x-2 \right)...\left( x-1000 \right)\). Tính \(f'\left( 0 \right)\) ?
Đáp án: B Phương pháp giải: Đạo hàm của hàm số \(y=f\left( x \right)\) tại điểm \(x={{x}_{0}}\) là \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) Lời giải chi tiết: \(\begin{array}{l}f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 1000} \right) - 0}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 1000} \right) = \mathop {\lim }\limits_{x \to 0} \left( { - 1} \right)\left( { - 2} \right)\left( { - 3} \right)...\left( { - 1000} \right) = {\left( { - 1} \right)^{1000}}.1000! = 1000!\end{array}\) Chọn B. Câu hỏi 22 : Tìm a, b để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 0\\a\sin x + b\cos x\,\,\,\,khi\,\,x < 0\end{array} \right.\) có đạo hàm tại điểm \({{x}_{0}}=0\).
Đáp án: A Phương pháp giải: +) Trước hết, tìm điều kiện để hàm số liên tục tại x = 0. +) Sử dụng công thức tính đạo hàm bằng định nghĩa. +) Hàm số có đạo hàm tại x = 0 \(\Leftrightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\Leftrightarrow a=1.\) Sử dụng công thức \(\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}=1\) . Lời giải chi tiết: Để hàm số có đạo hàm tại x = 1 thì trước hết hàm số phải liên tục tại x = 1. Ta có: \(f\left( 0 \right)=1\) \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {a{x^2} + bx + 1} \right) = 1 = f\left( 0 \right)\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {a\sin x + b\cos x} \right) = b\end{array}\) Để hàm số liên tục tại x = 1 thì \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( 0 \right)\Leftrightarrow b=1\) Khi đó ta có: \(f'\left( 0 \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\) \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{a{x^2} + x + 1 - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + 1} \right) = 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{a\sin x + \cos x - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{2a\sin \frac{x}{2}\cos \frac{x}{2} - 2{{\sin }^2}\frac{x}{2}}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin \frac{x}{2}}}{{\frac{x}{2}}}\mathop {\lim }\limits_{x \to {0^ - }} \left( {a\cos \frac{x}{2} - 2\sin \frac{x}{2}} \right) = a\end{array}\)Để tồn tại \(f'\left( 0 \right)\Leftrightarrow \underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}=\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\Leftrightarrow a=1.\) Chọn A. Câu hỏi 23 : Cho hàm số \(f\left( x \right)=\sqrt{{{x}^{2}}}\). Giá trị \(f'\left( 0 \right)\) bằng:
Đáp án: D Phương pháp giải: Sử dụng công thức đạo hàm của hàm số hợp \(\left( \sqrt{u} \right)'=\frac{u'}{2\sqrt{u}}\) Lời giải chi tiết: \(\begin{array}{l}f\left( x \right) = \left| x \right|\\\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \frac{x}{x} = 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \frac{{ - x}}{x} = - 1\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} \ne \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\end{array}\) Do đó không tồn tại \(f'\left( 0 \right)\) của hàm số trên. Chọn D. Câu hỏi 24 : Cho hàm số \(y = f\left( x \right)\) xác định trên tập số thực R thỏa mãn \(\mathop {\lim }\limits_{x \to 2} {{f\left( x \right) - f\left( 2 \right)} \over {x - 2}} = 3\). Kết quả nào sau đây là đúng?
Đáp án: B Phương pháp giải: Sử dụng công thức tính đạo hàm bằng định nghĩa \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to 2} {{f\left( x \right) - f\left( 2 \right)} \over {x - 2}} = 3 \Rightarrow f'\left( 2 \right) = 3\) Chọn B. Câu hỏi 25 : Cho hàm số \(y = f\left( x \right)\) xác định trên tập số thực R, có đạo hàm tại \(x = - 1\). Định nghĩa về đạo hàm nào sau đây là đúng?
Đáp án: C Phương pháp giải: Sử dụng công thức tính đạo hàm bằng định nghĩa \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to - 1} {{f\left( x \right) - f\left( { - 1} \right)} \over {x + 1}} = f'\left( { - 1} \right)\). Chọn C. Câu hỏi 26 : Cho hàm số \(y=f\left( x \right)\) có đạo hàm thỏa mãn \(f'\left( 6 \right)=2\). Giá trị biểu thức \(\underset{x\to 6}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 6 \right)}{x-6}\) bằng:
Đáp án: A Phương pháp giải: Sử dụng công thức tính đạo hàm bằng định nghĩa: \(f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\) (nếu tồn tại giới hạn). Lời giải chi tiết: Ta có: \(f'\left( 6 \right)=\underset{x\to 6}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 6 \right)}{x-6}=2\) Chọn A. Câu hỏi 27 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \({x_0}\) là \(f'\left( {{x_0}} \right)\). Khẳng định nào sau đây sai?
Đáp án: B Phương pháp giải: Sử dụng định nghĩa tính đạo hàm của một hàm số. Lời giải chi tiết: Chọn B. Câu hỏi 28 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {3x + 1} - 2x}}{{x - 1}}\,\,khi\,\,x \ne 1\\ - \dfrac{5}{4}\,\,\,\,khi\,x = 1\end{array} \right.\). Tính \(f'\left( 1 \right)\).
Đáp án: C Phương pháp giải: +) Kiểm tra tính liên tục của hàm số tại \(x = 1\). +) Nếu hàm số liên tục tại \(x = 1\), sử dụng công thức tính đạo hàm bằng định nghĩa: \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\). Lời giải chi tiết: Trước hết ta xét tính liên tục của hàm số tại \(x = 1\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{\sqrt {3x + 1} - 2x}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {\sqrt {3x + 1} - 2x} \right)\left( {\sqrt {3x + 1} + 2x} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {3x + 1} + 2x} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{3x + 1 - 4{x^2}}}{{\left( {x - 1} \right)\left( {\sqrt {3x + 1} + 2x} \right)}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{ - \left( {x - 1} \right)\left( {4x + 1} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {3x + 1} + 2x} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{ - 4x - 1}}{{\sqrt {3x + 1} + 2x}} = \dfrac{{ - 4 - 1}}{{\sqrt 4 + 2}} = \dfrac{{ - 5}}{4} = f\left( 1 \right)\end{array}\) \( \Rightarrow \) Hàm số liên tục tại \(x = 1\). Tính \(f'\left( 1 \right)\). \(\begin{array}{l} \Rightarrow f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \dfrac{{\dfrac{{\sqrt {3x + 1} - 2x}}{{x - 1}} + \dfrac{5}{4}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{4\sqrt {3x + 1} - 8x + 5x - 5}}{{4{{\left( {x - 1} \right)}^2}}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{4\sqrt {3x + 1} - 3x - 5}}{{4{{\left( {x - 1} \right)}^2}}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {4\sqrt {3x + 1} - 3x - 5} \right)\left( {4\sqrt {3x + 1} + 3x + 5} \right)}}{{4{{\left( {x - 1} \right)}^2}\left( {4\sqrt {3x + 1} + 3x + 5} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{16\left( {3x + 1} \right) - \left( {9{x^2} + 30x + 25} \right)}}{{4{{\left( {x - 1} \right)}^2}\left( {4\sqrt {3x + 1} + 3x + 5} \right)}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{ - 9{x^2} + 18x - 9}}{{4{{\left( {x - 1} \right)}^2}\left( {4\sqrt {3x + 1} + 3x + 5} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{ - 9{{\left( {x - 1} \right)}^2}}}{{4{{\left( {x - 1} \right)}^2}\left( {4\sqrt {3x + 1} + 3x + 5} \right)}} = \mathop {\lim }\limits_{x \to 1} \dfrac{{ - 9}}{{4\left( {4\sqrt {3x + 1} + 3x + 5} \right)}} = \dfrac{{ - 9}}{{64}}\end{array}\) Chọn C. Câu hỏi 29 : Xét 2 mệnh đề sau: (I): Nếu hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \(x = {x_0}\) thì \(y = f\left( x \right)\) liên tục tại điểm đó. (II): Nếu hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) thì \(y = f\left( x \right)\) có đạo hàm tại điểm đó. (III): Nếu hàm số \(y = f\left( x \right)\) gián đoạn tại điểm \(x = {x_0}\) thì chắc chắn \(y = f\left( x \right)\) không có đạo hàm tại điểm đó.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Nếu hàm số \(y = f\left( x \right)\) có đạo hàm tại điểm \(x = {x_0}\) thì \(y = f\left( x \right)\) liên tục tại điểm đó và nếu hàm số \(y = f\left( x \right)\) gián đoạn tại điểm \(x = {x_0}\) thì chắc chắn \(y = f\left( x \right)\) không có đạo hàm tại điểm đó là 2 mệnh đề đúng. Chọn B. Câu hỏi 30 : Cho hàm \(f\left( x \right)\) liên tục trên khoảng \(\left( {a;b} \right)\), \({x_0} \in \left( {a;b} \right)\). Tính\(f'\left( {{x_0}} \right)\) bằng định nghĩa ta cần tính :
Đáp án: B Phương pháp giải: Sử dụng công thức tính đạo hàm bằng định nghĩa. Lời giải chi tiết: Tính\(f'\left( {{x_0}} \right)\) bằng định nghĩa ta cần tính \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}\). Chọn B. Câu hỏi 31 : Tìm số gia \(\Delta y\) của hàm số \(y = {x^2}\) biết \({x_0} = 3\) và \(\Delta x = - 1.\)
Đáp án: C Phương pháp giải: Số gia \(\Delta y\) của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) ứng với số gia \(\Delta x\) là \(\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\). Lời giải chi tiết: Đặt \(y = {x^2} = f\left( x \right)\) ta có: \(\begin{array}{l}\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right) = f\left( {3 - 1} \right) - f\left( 3 \right)\\\,\,\,\,\,\,\, = f\left( 2 \right) - f\left( 3 \right) = {2^2} - {3^2} = - 5\end{array}\) Chọn C. Câu hỏi 32 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên tập số thực. Tìm hệ thức đúng?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hệ thức đúng là: \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}.\) Chọn A. Câu hỏi 33 : Cho hàm số \(f\left( x \right) = \sqrt {x + 1} \). Tính đạo hàm của hàm số tại điểm \({x_0} = 1\).
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: TXĐ: \(D = \left[ { - 1; + \infty } \right)\) \(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 1} - \sqrt 2 }}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{x + 1 - 2}}{{\left( {x - 1} \right)\left( {\sqrt {x + 1} + \sqrt 2 } \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 1} + \sqrt 2 }} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\end{array}\) Chọn A. Câu hỏi 34 : Khi tính đạo hàm của hàm số \(f\left( x \right) = {x^2} + 5x - 3\) tại điểm \({x_0} = 2\), một học sinh đã tính theo các bước sau: Bước 1: \(f\left( x \right) - f\left( 2 \right) = f\left( x \right) - 11\) Bước 2: \(\frac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \frac{{{x^2} + 5x - 3 - 11}}{{x - 2}} = \frac{{\left( {x - 2} \right)\left( {x + 7} \right)}}{{x - 2}} = x + 7\) Bước 3: \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 7} \right) = 9 \Rightarrow f'\left( 2 \right) = 9\) Tính toán trên nếu sai thì sai ở bước nào?
Đáp án: D Phương pháp giải: Xét tính đúng sai ở từng bước. Lời giải chi tiết: Bài giải trên hoàn toàn đúng. Chọn D. Câu hỏi 35 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3 - \sqrt {4 - x} \,\,\,khi\,\,x \ne 0\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Khi đó \(f'\left( 0 \right)\) là kết quả nào sau đây?
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\begin{array}{l}f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{3 - \sqrt {4 - x} - 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{2 - \sqrt {4 - x} }}{x}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{4 - 4 + x}}{{x\left( {2 + \sqrt {4 - x} } \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{2 + \sqrt {4 - x} }} = \frac{1}{4}\end{array}\) Chọn A. Câu hỏi 36 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\\\frac{{{x^3} + 2{x^2} - 7x + 4}}{{x - 1}}\,\,khi\,\,x < 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x + 3 - 5}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 2}}{{x - 1}} = 2\\\mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\frac{{{x^3} + 2{x^2} - 7x + 4}}{{x - 1}} - 5}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^3} + 2{x^2} - 12x + 9}}{{{{\left( {x - 1} \right)}^2}}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{\left( {x - 1} \right)\left( {{x^2} + 3x - 9} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} + 3x - 9}}{{x - 1}} = + \infty \\ \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} \ne \mathop {\lim }\limits_{x \to {1^ - }} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\end{array}\) Vậy hàm số không tồn tại đạo hàm tại x = 1. Chọn D. Câu hỏi 37 : Cho hàm số \(y = f\left( x \right)\) xác định: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} + 1} - 1}}{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:
Đáp án: A Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: \(\begin{array}{l}f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sqrt {{x^2} + 1} - 1}}{x}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} - 1}}{{{x^2}}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} + 1 - 1}}{{{x^2}\left( {\sqrt {{x^2} + 1} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {{x^2} + 1} + 1}} = \frac{1}{2}\end{array}\) Chọn A. Câu hỏi 38 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{4{x^2} + 8}} - \sqrt {8{x^2} + 4} }}{{{x^2}}}\,\,\,khi\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:
Đáp án: B Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: Để hàm số có đạo hàm tại x = 0, trước hết hàm số phải liên tục tại x = 0. \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{4{x^2} + 8}} - \sqrt {8{x^2} + 4} }}{{{x^2}}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{4{x^2} + 8}} - 2}}{{{x^2}}} - \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {8{x^2} + 4} - 2}}{{{x^2}}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{{4{x^2}}}{{{x^2}\left( {{{\sqrt[3]{{4{x^2} + 8}}}^2} + 2\sqrt[3]{{4{x^2} + 8}} + 4} \right)}} - \mathop {\lim }\limits_{x \to 0} \frac{{8{x^2}}}{{{x^2}\left( {\sqrt {8{x^2} + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \frac{4}{{{{\sqrt[3]{{4{x^2} + 8}}}^2} + 2\sqrt[3]{{4{x^2} + 8}} + 4}} - \mathop {\lim }\limits_{x \to 0} \frac{8}{{\sqrt {8{x^2} + 4} + 2}} = \frac{1}{3} - 2 = - \frac{5}{3}\end{array}\) Chọn B. Câu hỏi 39 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 4{x^2} + 3x}}{{{x^2} - 3x + 2}}\,\,\,khi\,\,x \ne 1\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:
Đáp án: D Phương pháp giải: Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại). Lời giải chi tiết: Ta có: \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{{{x^3} - 4{x^2} + 3x}}{{{x^2} - 3x + 2}}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{x\left( {x - 3} \right)\left( {x - 1} \right)}}{{{{\left( {x - 1} \right)}^2}\left( {x - 2} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{x\left( {x - 3} \right)}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} = - \infty \) Vậy hàm số không có đạo hàm tại x = 1. Chọn D. Câu hỏi 40 : Tìm a, b để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} + 1}}{{x + 1}}\,\,khi\,\,x \ge 0\\ax + b\,\,khi\,\,x < 0\end{array} \right.\) có đạo hàm tại điểm \(x = 0.\)
Đáp án: D Phương pháp giải: +) Trước hết hàm số liên tục tại x = 0. +) Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \Leftrightarrow f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x}\) Lời giải chi tiết: Trước tiên hàm số phải liên tục tại x = 0. Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2} + 1}}{{x + 1}} = 1\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {ax + b} \right) = b = f\left( 0 \right)\end{array}\) Để hàm số liên tục tại x = 0 thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow b = 1\) Khi đó ta có \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{x}\) Ta có \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\frac{{{x^2} + 1}}{{x + 1}} - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2} - x}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{x - 1}}{{x + 1}} = - 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left( {ax + 1} \right) - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} a = a\end{array}\) Để hàm số có đạo hàm tại x = 0 thì \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} \Leftrightarrow a = - 1\) Vậy \(a = - 1,b = 1\). Chọn D. Câu hỏi 41 : Tìm a, b để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 0\\a\sin x + b\cos x\,\,\,\,khi\,\,x < 0\end{array} \right.\) có đạo hàm tại điểm \({x_0} = 0\).
Đáp án: A Phương pháp giải: +) Trước hết, tìm điều kiện để hàm số liên tục tại x = 0. +) Sử dụng công thức tính đạo hàm bằng định nghĩa. +) Hàm số có đạo hàm tại \(x = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} \Leftrightarrow a = 1.\) Sử dụng công thức \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\) . Lời giải chi tiết: Để hàm số có đạo hàm tại x = 1 thì trước hết hàm số phải liên tục tại x = 1. Ta có: \(f\left( 0 \right) = 1\) \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {a{x^2} + bx + 1} \right) = 1 = f\left( 0 \right)\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {a\sin x + b\cos x} \right) = b\end{array}\) Để hàm số liên tục tại x = 1 thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow b = 1\) Khi đó ta có: \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{a{x^2} + x + 1 - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + 1} \right) = 1\\\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{a\sin x + \cos x - 1}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{2a\sin \frac{x}{2}\cos \frac{x}{2} - 2{{\sin }^2}\frac{x}{2}}}{x}\\ = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{\sin \frac{x}{2}}}{{\frac{x}{2}}}\mathop {\lim }\limits_{x \to {0^ - }} \left( {a\cos \frac{x}{2} - 2\sin \frac{x}{2}} \right) = a\end{array}\) Để tồn tại \(f'\left( 0 \right) \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} \Leftrightarrow a = 1.\) Chọn A. Câu hỏi 42 : Tính đạo hàm của hàm số sau: \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - 3x + 1\,\,\,\,khi\,\,x > 1\\2x + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\) ta được:
Đáp án: B Phương pháp giải: +) Tính đạo hàm của hàm số khi \(x > 1\) +) Tính đạo hàm của hàm số khi \(x < 1\) +) Sử dụng định nghĩa đạo hàm, xét sự tồn tại của đạo hàm của hàm số tại x = 1. Lời giải chi tiết: Với \(x > 1\) ta có: \(f\left( x \right) = {x^2} - 3x + 1 \Rightarrow f'\left( x \right) = 2x - 3\) Với \(x < 1\) ta có : \(f\left( x \right) = 2x + 2 \Leftrightarrow f'\left( x \right) = 2\) Với x = 1 ta có : \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} - 3x + 1} \right) = - 1 \ne f\left( 1 \right) = 4 \Rightarrow \) Hàm số không liên tục tại \(x = 1,\) do đó không có đạo hàm tại \(x = 1.\) Vậy \(f'\left( x \right) = \left\{ \begin{array}{l}2x - 3\,\,\,khi\,\,x > 1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x < 1\end{array} \right.\) Chọn B. Câu hỏi 43 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {1 - x} - 1}}{x}\,\,khi\,\,x \ne 0,\,\,x \le 1\\\,\,\,\,\,\,\,\,a\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Tìm \(a\) để hàm số có đạo hàm tại \(x = 0\) và tính đạo hàm tại điểm đó.
Đáp án: A Phương pháp giải: - Tìm \(a\) để hàm số liên tục tại \(x = 0\). - Với giá trị \(a\) vừa tìm được, tính \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\), xét xem đạo hàm có tồn tại hay không (giới hạn có hữu hạn hay không). Lời giải chi tiết: TXĐ: \(D = \left( { - \infty ;1} \right],\,\,x = 0 \in D\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 - x} - 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{ - x}}{{x\left( {\sqrt {1 - x} + 1} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \frac{{ - 1}}{{\sqrt {1 - x} + 1}} = \frac{{ - 1}}{2}\\f\left( 0 \right) = a\end{array}\) Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - \frac{1}{2}\). Khi đó ta có: \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {1 - x} - 1}}{x}\,\,khi\,\,x \ne 0,\,\,x \le 1\\\,\,\,\,\,\, - \frac{1}{2}\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). \(\begin{array}{l} Vậy để hàm số có đạo hàm tại \(x = 0\) thì \(a = - \frac{1}{2}\). Chọn A. Câu hỏi 44 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + a\,\,\,khi\,\,x \ge - 1\\{x^2} + bx\,\,\,\,khi\,\,x < - 1\end{array} \right.\). Tìm \(a,\,\,b\) để hàm số có đạo hàm tại \(x = - 1\).
Đáp án: B Phương pháp giải: - Tìm \(a\) để hàm số liên tục tại \(x = - 1\), từ đó rút \(b\) theo \(a\). - Tính \(f'\left( { - {1^ + }} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\), \(f'\left( { - {1^ - }} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\) . - Để hàm số tồn tại đạo hàm tại \(x = - 1\) thì \(f'\left( { - {1^ + }} \right) = f'\left( { - {1^ - }} \right)\). Lời giải chi tiết: TXĐ: \(D = \mathbb{R},\,\,x = - 1 \in D\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - {x^2} + a} \right) = a - 1 = f\left( { - 1} \right)\\\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {{x^2} + bx} \right) = 1 - b\end{array}\) Để hàm số liên tục tại \(x = - 1\) thì \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = f\left( { - 1} \right)\)\( \Leftrightarrow a - 1 = 1 - b \Leftrightarrow a + b = 2\). Tính đạo hàm tại điểm \(x = - 1\): \(\begin{array}{l}f'\left( { - {1^ + }} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{ - {x^2} + a - \left( { - 1 + a} \right)}}{{x + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{ - {x^2} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - x + 1} \right) = 2\\f'\left( { - {1^ - }} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + bx - \left( { - 1 + a} \right)}}{{x + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + bx + 1 - a}}{{x + 1}}\end{array}\) Thay \(a = 2 - b\) ta có: \(\begin{array}{l}f'\left( { - {1^ - }} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + bx - 1 + b}}{{x + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\left( {x - 1} \right)\left( {x + 1} \right) + b\left( {x + 1} \right)}}{{x + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {x - 1 + b} \right) = b - 2\end{array}\). Để hàm số có đạo hàm tại \(x = - 1\) thì \(f'\left( { - {1^ + }} \right) = f'\left( { - {1^ - }} \right)\)\( \Leftrightarrow b - 2 = 2 \Leftrightarrow b = 4\)\( \Rightarrow a = -2\). Vậy \(a = -2,\,\,b = 4\). Chọn B. Câu hỏi 45 : Điện lượng trong một dây dẫn biểu diễn theo phương trình \(Q = 2{t^2} + t\) (\(t\): giây, \(Q\): culông). Tính cường độ dòng điện tại thời điểm \(t = 4s\).
Đáp án: C Phương pháp giải: \(I\left( 4 \right) = Q'\left( 4 \right) = \mathop {\lim }\limits_{t \to 4} \frac{{Q\left( t \right) - Q\left( 4 \right)}}{{t - 4}}\) Lời giải chi tiết: \(I\left( 4 \right) = Q'\left( 4 \right) = \mathop {\lim }\limits_{t \to 4} \frac{{Q\left( t \right) - Q\left( 4 \right)}}{{t - 4}}\). \( = \mathop {\lim }\limits_{t \to 4} \frac{{2{t^2} + t - 36}}{{t - 4}} = \mathop {\lim }\limits_{t \to 4} \frac{{\left( {t - 4} \right)\left( {2t + 9} \right)}}{{t - 4}} = \mathop {\lim }\limits_{t \to 4} \left( {2t + 9} \right) = 17\,\,\left( A \right)\). Chọn C. Câu hỏi 46 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx + 1\,\,\,khi\,\,x \ge 0\\ax - b - 1\,\,\,\,\,\,\,khi\,\,x < 0\end{array} \right.\). Khi hàm số \(f\left( x \right)\) có đạo hàm tại \({x_0} = 0\). Hãy tính \(T = a - 2b\).
Đáp án: C Phương pháp giải: - Tìm điều kiện để hàm số liên tục tại \(x = 0\): \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right)\). - Tìm điều kiện để hàm số có đạo hàm tại \(x = 0\): \(f'\left( {{0^ + }} \right) = f'\left( {{0^ - }} \right)\), với \(f\left( {{0^ \pm }} \right) = \mathop {\lim }\limits_{x \to {0^ \pm }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Lời giải chi tiết: TXĐ: \(D = \mathbb{R},\,\,x = 0 \in D\). Để hàm số có đạo hàm tại \({x_0} = 0\), trước hết hàm số phải liên tục tại \(x = 0\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {a{x^2} + bx + 1} \right) = 1 = f\left( 0 \right)\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {ax - b - 1} \right) = - b - 1\end{array}\) Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right)\) \( \Leftrightarrow - b - 1 = 1 \Leftrightarrow b = - 2\). Ta có: \(\begin{array}{l}f'\left( {{0^ + }} \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{a{x^2} + bx + 1 - 1}}{x}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + b} \right) = b = - 2\\f'\left( {{0^ - }} \right) = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ax - b - 1 - 1}}{x}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{ax}}{x} = a\end{array}\) Để hàm số có đạo hàm tại \(x = 0\) thì \(f'\left( {{0^ + }} \right) = f'\left( {{0^ - }} \right)\) \( \Leftrightarrow a = - 2\). Vậy \(T = a - 2b = - 2 - 2.\left( { - 2} \right) = 2\). Chọn C. Câu hỏi 47 : Số gia \(\Delta y\) của hàm số \(y = {x^2} + 2x\) tại điểm \({x_0} = 1\) là:
Đáp án: B Phương pháp giải: Sử dụng công thức tính số gia của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là: \(\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\). Lời giải chi tiết: \(\begin{array}{l}\Delta y = f\left( {1 + \Delta x} \right) - f\left( 1 \right)\\\,\,\,\,\,\,\, = {\left( {1 + \Delta x} \right)^2} + 2\left( {1 + \Delta x} \right) - {1^2} - 2.1\\\,\,\,\,\,\,\, = {\left( {\Delta x} \right)^2} + 2\Delta x + 1 + 2 + 2\Delta x - 3\\\,\,\,\,\,\,\, = {\Delta ^2}x + 4\Delta x\end{array}\) Chọn B. Câu hỏi 48 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^3} + 2{x^2} + 3bx + 2\,\,\,khi\,\,x > 1\\\sqrt {5 - 4x} - 2x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\). Hàm số có đạo hàm tại \(x = 1\) thì giá trị \(ab\) bằng:
Đáp án: C Phương pháp giải: - Tìm điều kiện để hàm số liên tục tại \(x = 1\). - Tính \(f'\left( {{1^ \pm }} \right) = \mathop {\lim }\limits_{x \to {1^ \pm }} \dfrac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\). - Để hàm số có đạo hàm tại \(x = 1\) thì \(f'\left( {{1^ + }} \right) = f'\left( {{1^ - }} \right)\). Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {a{x^3} + 2{x^2} + 3bx + 2} \right) = a + 3b + 4\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {\sqrt {5 - 4x} - 2x} \right) = - 1 = f\left( 1 \right)\end{array}\) Để hàm số có đại hàm tại \(x = 1\) thì hàm số phải liên tục tại \(x = 1\)\( \Rightarrow a + 3b + 4 = - 1 \Leftrightarrow a + 3b = - 5\,\,\,\left( 1 \right)\). Ta có: \(\begin{array}{l}f'\left( {{1^ - }} \right) = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{\sqrt {5 - 4x} - 2x + 1}}{{x - 1}} = - 4\\f'\left( {{1^ + }} \right) = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{a{x^3} + 2{x^2} + 3bx + 2 + 1}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\left( { - 5 - 3b} \right){x^3} + 2{x^2} + 3bx + 3}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\left( { - 5 - 3b} \right){x^3} + 2{x^2} - 2 + 3bx - 3b + 3b + 5}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\left( { - 5 - 3b} \right)\left( {{x^3} - 1} \right) + 2\left( {x - 1} \right)\left( {x + 1} \right) + 3b\left( {x - 1} \right)}}{{x - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {1^ + }} \left[ {\left( { - 5 - 3b} \right)\left( {{x^2} + x + 1} \right) + 2\left( {x + 1} \right) + 3b} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3\left( { - 5 - 3b} \right) + 4 + 3b = - 6b - 11\end{array}\) Để hàm số có đạo hàm tại \(x = 1\) thì \(f'\left( {{1^ + }} \right) = f'\left( {{1^ - }} \right)\)\( \Leftrightarrow - 6b - 11 = - 4 \Leftrightarrow b = \dfrac{{ - 7}}{6}\). Thay vào (1) ta có: \(a + 3.\dfrac{{ - 7}}{6} = - 5 \Leftrightarrow a = - \dfrac{3}{2}\) Vậy \(ab = - \dfrac{3}{2}.\dfrac{{ - 7}}{6} = \dfrac{7}{4}\). Chọn C. Câu hỏi 49 : Đạo hàm của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{x^3} + 2{x^2} + x + 4} - 2}}{{x + 1}}\,\,\,khi\,\,x \ne - 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = - 1\end{array} \right.\) tại \(x = - 1\) là:
Đáp án: A Phương pháp giải: - Xét tính liên tục của hàm số tại \(x = - 1\). - Tính \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\). Lời giải chi tiết: Ta có: \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{{\sqrt {{x^3} + 2{x^2} + x + 4} {\rm{\;}} - 2}}{{x + 1}}\). \(\begin{array}{l} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^3} + 2{x^2} + x + 4 - 4}}{{\left( {x + 1} \right)\left( {\sqrt {{x^3} + 2{x^2} + x + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{{x{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {\sqrt {{x^3} + 2{x^2} + x + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{{x\left( {x + 1} \right)}}{{\sqrt {{x^3} + 2{x^2} + x + 4} + 2}} = 0 = f\left( { - 1} \right)\end{array}\) \( \Rightarrow \) Hàm số đã cho liên tục tại \(x = - 1\). Ta có: \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{\sqrt {{x^3} + 2{x^2} + x + 4} {\rm{\;}} - 2}}{{{{\left( {x + 1} \right)}^2}}}\) \(\begin{array}{l} = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^3} + 2{x^2} + x + 4 - 4}}{{{{\left( {x + 1} \right)}^2}\left( {\sqrt {{x^3} + 2{x^2} + x + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{{x{{\left( {x + 1} \right)}^2}}}{{{{\left( {x + 1} \right)}^2}\left( {\sqrt {{x^3} + 2{x^2} + x + 4} + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{x}{{\sqrt {{x^3} + 2{x^2} + x + 4} + 2}} = \dfrac{{ - 1}}{4}\end{array}\) Chọn A. Câu hỏi 50 : Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{2 - \sqrt {4 - x} }}{x}\,\,khi\,\,x \ne 0\\\,\,\,\,\,\,\,\dfrac{1}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Khi đó \(f'\left( 0 \right)\) là kết quả nào trong các kết quả sau:
Đáp án: C Phương pháp giải: - Xét tính liên tục của hàm số tại \(x = 0\). - Tính giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Nếu giới hạn này tồn tại thì \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Lời giải chi tiết: Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{2 - \sqrt {4 - x} }}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{{4 - 4 + x}}{{x\left( {2 + \sqrt {4 - x} } \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \dfrac{1}{{2 + \sqrt {4 - x} }} = \dfrac{1}{{2 + 2}} = \dfrac{1}{4}\\ \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\end{array}\) \( \Rightarrow \) Hàm số đã cho liên tục tại \(x = 0\). Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\dfrac{{2 - \sqrt {4 - x} }}{x} - \dfrac{1}{4}}}{x}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \dfrac{{8 - 4\sqrt {4 - x} - x}}{{4{x^2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \dfrac{{{{\left( {8 - x} \right)}^2} - 16\left( {4 - x} \right)}}{{4{x^2}\left( {8 - x + 4\sqrt {4 - x} } \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \dfrac{{{x^2} - 16x + 64 - 64 + 16x}}{{4{x^2}\left( {8 - x + 4\sqrt {4 - x} } \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to 0} \dfrac{1}{{4\left( {8 - x + 4\sqrt {4 - x} } \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{{4\left( {8 - 0 + 4.2} \right)}} = \dfrac{1}{{64}}\end{array}\) Vậy \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \dfrac{1}{{64}}\). Chọn C. Quảng cáo
|