Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 11

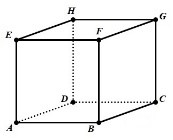
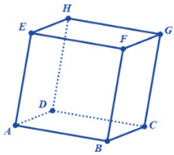
Đề bài

Câu 1: Cho hàm \(f\left( x \right)\) liên tục trên khoảng \(\left( {a;b} \right)\), \({x_0} \in \left( {a;b} \right)\). Tính\(f'\left( {{x_0}} \right)\) bằng định nghĩa ta cần tính :

A. \(\mathop {\lim }\limits_{x \to 0} \frac{{\Delta y}}{{\Delta x}}\). B. \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}\).

C. \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta x}}{{\Delta y}}\).  D. \(\mathop {\lim }\limits_{x \to 0} \frac{{\Delta y}}{x}\).

Câu 2: Chọn khẳng định sai trong các khẳng định sau:

A. Hàm số \(y = 5{x^3} + x - 2\) liên tục trên \(\mathbb{R}\).

B. Hàm số  \(y = \frac{{3x - 5}}{{x + 3}}\)  liên tục trên \(\mathbb{R}\).

C. Hàm số \(y = \frac{{2{x^2} - x}}{{x + 1}}\)  liên tục trên khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\)

D. Hàm số \(y = {x^5} + 3{x^3} + 5\)  liên tục trên \(\mathbb{R}\).

Câu 3: Cho hình lập phương \(ABCD.EFGH\)(tham khảo hình vẽ bên) có cạnh bằng 5 cm. Tính khoảng cách giữa 2 đường thẳng chéo nhau AD và HF ta được

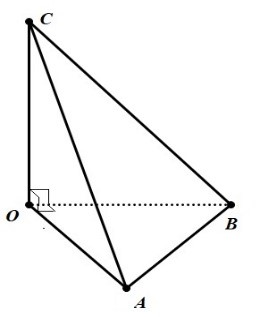
A. \(5\sqrt 3 \,cm\).       B. \(5\,cm\).

C. \(5\sqrt 2 \,cm\).        D. \(9\,cm\).

Câu 4: Tính đạo hàm của hàm số \(y = 2\sin x + 2020.\)

A. \(y' = 2\sin x\).

B. \(y' =  - 2\cos x\).

C. \(y' = 2\cos x\).

D. \(y' =  - 2\sin x\).

Câu 5: Trong các giới hạn dãy số dưới đây, giới hạn có kết quả đúng là:

A. \(\lim \,( - 3{n^4} + 3) =  - \infty \).

B. \(\lim \,( - 3{n^4} + 3) = 0\).

C. \(\lim \,( - {n^4} + 2) =  + \infty \).

D. \(\lim \,(5{n^4} - 2) =  - \infty \).

Câu 6: Cho hàm số \(y = {x^3} - 3x + 1.\) Tìm \(dy.\)

A. \(dy = ({x^2} - 1)dx\).

B. \(dy = ({x^3} - 3x + 1)dx\).

C. \(dy = (3{x^2} - 3)dx\).

D. \(dy = (3{x^3} - 3)dx\)

Câu 7: Tính \(\mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} + 3x - 1}}{{x + 1}}\). Kết quả đúng là:

A. \(3\)                               B. \(\frac{5}{2}\) .

C. \( - 2\).                          D. \(2\)

Câu 8: Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc (xem hình vẽ). Chọn khẳng định sai khi nói về hai mặt phẳng vuông góc.

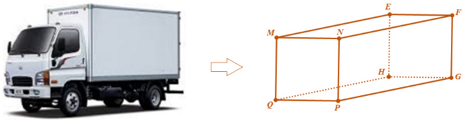
A. \((OAB) \bot (ABC)\).

B. \((OAB) \bot (OAC)\).

C. \((OBC) \bot (OAC)\).

D. \((OAB) \bot (OBC)\).

Câu 9: Container của xe tải dùng để chở hàng hóa thường có dạng hình hộp chữ nhật. Chúng ta mô hình hóa thùng container bằng hình hộp chữ nhật \(MNPQ.EFGH\) (tham khảo hình vẽ bên dưới). Chọn khẳng định sai khi nói về hai đường thẳng vuông góc trong các khẳng định sau.

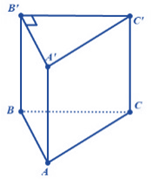
A. \(HE \bot NF\).

B. \(HE \bot MN\).

C. \(HE \bot GP\).

D. \(HE \bot QN\).

Câu 10: Cho hàm số\(f\left( x \right) = {x^3} - 3{x^2} + 1\). Tính \(f''\left( x \right)\).

A. \(f''\left( x \right) = 6x-6\).

B. \(f''\left( x \right) = x-1\).

C. \(f''\left( x \right) = {x^2} - 2x\).

D. \(f''\left( x \right) = 3{x^2} - 6x\).

Câu 11: Tính đạo hàm của hàm số \(f(x) = 3{x^3}\).

A. \(6{x^2}\).                  B. \({x^2}\).

C. \(6x\).        D. \(9{x^2}\).

Câu 12:  Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(\Delta A'B'C'\) vuông tại \(B'\)  (xem hình vẽ). Hỏi đường thẳng \(B'C'\) vuông góc với mặt phẳng nào được liệt kê ở bốn phương án dưới đây ?

A. \((BB'A')\).                 B. \((AA'C')\).

C. \((ABC)\).           D. \((ACC')\).

Câu 13: Cho hình hộp \(ABCD.EFGH\) (tham khảo hình vẽ). Tính tổng ba véctơ \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AE} \) ta được

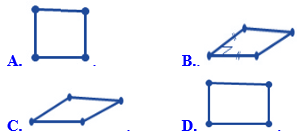
A. \(\overrightarrow {AG} \).                             B. \(\overrightarrow {AH} \).

C. \(\overrightarrow {AF} \).    D. \(\overrightarrow {AC} \).

Câu 14: Trong hình học không gian thì hình nào bên dưới là hình biểu diễn của hình vuông qua phép chiếu song song ?

Câu 15: Vi phân của hàm số\(y\,\, = \,\cos 2x + \cot x\) là:

A. \(dy\,\, = \,\,\left( { - 2\cos 2x + \frac{1}{{{{\sin }^2}x}}} \right)dx\)

B. \(dy\,\, = \,\,\left( {2\sin 2x + \frac{1}{{{{\sin }^2}x}}} \right)dx\).

C. \(dy\,\, = \,\,\left( { - 2\cos 2x - \frac{1}{{{{\sin }^2}x}}} \right)dx\).

D. \(dy\,\, = \,\,\left( { - 2\sin 2x - \frac{1}{{{{\sin }^2}x}}} \right)dx\).

Câu 16: Chọn kết quả đúng trong các giới hạn dưới đây:

A. \(\lim \frac{{3{n^2} - 14}}{{10n + 2}} = \frac{3}{{10}}\).

B. \(\lim \frac{{5n - 4}}{{{n^2} - 1}} = 5\).

C. \(\lim \frac{{ - 2{n^2} - 1}}{{5{n^2} - 8}} =  - \frac{2}{5}\).

D. \(\lim \frac{{{n^2} - 5}}{{n + 4}} = 0\).

Câu 17: Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} + x - 12}}{{x - 3}}\). Kết quả đúng là:

A. \( - 7\).                          B. \(0\)

C. \(7\)                               D. \( - 1\).

Câu 18: Cho đường thẳng d vuông góc với mặt phẳng \((\alpha )\) và đường thẳng \(\Delta \) khác d. Chọn khẳng định sai trong các khẳng định sau.

A. Đường thẳng \(\Delta \,{\rm{//}}\,d\) thì \(\Delta  \bot (\alpha )\).

B. Đường thẳng \(\Delta \,{\rm{//}}\,d\) thì \(\Delta \,{\rm{//}}\,(\alpha )\).

C. Đường thẳng \(\Delta \,{\rm{//}}\,(\alpha )\) thì \(\Delta \, \bot \,d\).

D. Đường thẳng \(\Delta  \bot (\alpha )\)  thì \(\Delta \,{\rm{//}}\,d\).

Câu 19: Chọn khẳng định sai trong các khẳng định sau ?

A. Hai mặt phẳng vuông góc thì chúng cắt nhau.

B. Hai mặt phẳng cắt nhau thì không vuông góc.

C. Hai mặt phẳng vuông góc thì góc của chúng bằng \(90^\circ \).

D. Hai mặt phẳng có góc bằng \(90^\circ \) thì chúng vuông góc.

Câu 20: Cho hàm số\(f\left( x \right) = {\left( {2x + 1} \right)^{12}}\). Tính \(f''\left( 0 \right)\).

A. \(f''\left( x \right) = 132\).

B. \(f''\left( 0 \right) = 528\). 

C. \(f''\left( 0 \right) = 240\).  

D. \(f''\left( 0 \right) = 264\). 

Câu 21: Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) tại điểm có hoành độ \({x_0} = 0\) là:

A. \(1\).                              B. \( - 2\).

C. \( - 1\).                          D. \(2\).

Câu 22: Tìm số gia \(\Delta y\) của hàm số \(y = {x^2}\) biết \({x_0} = 3\) và \(\Delta x =  - 1.\)

A. \(\Delta y = 13\).       B. \(\Delta y = 7\).

C. \(\Delta y =  - 5\).      D. \(\Delta y = 16\) .

Câu 23: Tính \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 4}  + x} \right)\). Kết quả đúng là:

A. \(0\)                               B. \( - \infty \).

C. \( + \infty \).                D. \(2\)

Câu 24: Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng 6 cm. Tính khoảng cách từ điểm B đến mặt phẳng \((SCD)\)

A. \(5\sqrt 6 \,cm\). B. \(15\sqrt 6 \,cm\).

C. \(2\sqrt 6 \,cm\). D. \(4\sqrt 6 \,cm\).

Câu 25: Cho hàm số \(y = \frac{{{x^2} + 3}}{{x + 1}}\). Nếu\(y' > 0\) thì x thuộc tập hợp nào sau đây:

A. \(\left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\).

B. \(\left( { - 3; - 1} \right) \cup \left( {1; + \infty } \right)\).

C. \(\left( { - \infty ; - 3} \right) \cup \left( { - 1;1} \right)\).

D. \(\left( { - 3; - 1} \right) \cup \left( { - 1;1} \right)\).

Câu 26: Chọn kết quả sai trong các giới hạn dưới đây:

A. \(\lim \frac{{{{5.4}^n} + {{7.2}^n} - {3^n}}}{{{{4.4}^n} - {{2.3}^n}}} = \frac{5}{4}\).

B. \(\lim \frac{{\sqrt {9{n^2} + 4}  - n}}{{{n^2}}} = 0\).

C. \(\lim \frac{{{3^n} + {{4.5}^n} - {8^n}}}{{{{3.8}^n} + {{2.6}^n}}} =  - \frac{1}{3}\).

D. \(\lim \frac{{\sqrt {{n^2} + 4}  + n}}{n} = 3\).

Câu 27: Cho hàm số \(y = \cos \sqrt {2{x^2} - x + 7} \). Khi đó \(y'\) bằng  

A. \(y' =  - \sin \sqrt {2{x^2} - x + 7} \).

B. \(y' = (1 - 4x)\sin \sqrt {2{x^2} - x + 7} \).

C. \(y' = \frac{{\left( {1 - 4x} \right)\sin \sqrt {2{x^2} - x + 7} }}{{2\sqrt {2{x^2} - x + 7} }}\).

D. \(y' = \left( {2{x^2} - x + 7} \right)\sin \sqrt {2{x^2} - x + 7} \).

Câu 28: Cho hình chóp tam giác \(S.ABC\) có mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt đáy.  Biết góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy bằng \({60^0}\) cạnh \(AB = 4cm;\,\,BC = 6cm;\,\,CA = 8cm\). Tính độ dài cạnh SA của hình chóp.

A. \(\sqrt 5 \,cm\).          B. \(2\sqrt 3 \,cm\).

C. \(6\sqrt 3 \,cm\).        D. \(3\sqrt 5 \,cm\).

Câu 29: Gọi (C) là đồ thị của hàm số\(y = {(x - 1)^3}\). Tiếp tuyến của (C) song song với đường thẳng \(\Delta :12x - y - 2018 = 0\) có phương trình là:

A. \(y =  - 12x - 4\) và \(y =  - 12x + 4.\)

B. \(y = 12x + 28\) và \(y = 12x - 4\).

C. \(y =  - 12x - 28\) và \(y = 12x + 28\).

D. \(y = 12x - 28\) và  \(y = 12x + 4\).

Câu 30:  Cho hàm số \(f(x) = \left\{ \begin{array}{l}2b{x^2} - 4\,\,\,khi\,\,\,x \le 3\\\,\,\,\,\,5\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x > 3\end{array} \right.\). Hàm số liên tục trên \(\mathbb{R}\) khi giá trị của b  là:

A. \(\frac{1}{{18}}\) .    B.  \(2\)

C. \(18\)                             D.  \(\frac{1}{2}\).

II. PHẦN TỰ LUẬN (4.0 điểm) (Học sinh viết bài làm vào giấy, ghi rõ mã đề)

Bài 1: (1,0 điểm) Tính các giới hạn sau:

a) \(\lim \frac{{4n + 9}}{{6n - 7}}\)

b) \(\mathop {\lim }\limits_{x \to \, - 2} \frac{{2 - 5x - 3{x^2}}}{{2x + 4}}\).

Bài 2: (1,0 điểm) Tính đạo hàm của các hàm số:

a)\(y = {x^3} + 4{x^2} - 2x + 1\) tại \({x_0} =  - 4\)

b) \(y = \sqrt {7 + 5{{\cot }^4}{x^4}} \)

Bài 3: (0,5 điểm) Cho hàm của các hàm số

\(y = \frac{{m-1}}{{12}}{x^4}-\frac{{m + 1}}{3}{x^3}\)\( + \frac{{{\rm{3(}}m - 2)}}{2}{x^2} + 7x + 2020\)

Tìm \(m\) để  \(y'' < 0\) vô nghiệm.

Bài 4: (1,5 điểm) Cho hình chóp \(S.ABCD\), có \(ABCD\) là hình vuông tâm O  có cạnh \(a\), \(SA = a\sqrt 5 \) và \(SA \bot \left( {ABCD} \right)\).       

a) Chứng minh rằng:  \(CD \bot \left( {SAD} \right)\).

b) Chứng minh rằng:  \(\left( {SAC} \right) \bot \left( {SBD} \right)\).

c) Tính khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\).

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM

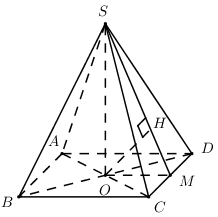
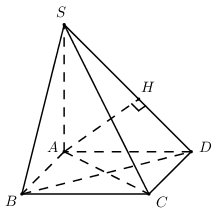
Câu 1 (NB):

Phương pháp:

Sử dụng công thức tính đạo hàm bằng định nghĩa.

Cách giải:

Tính\(f'\left( {{x_0}} \right)\) bằng định nghĩa ta cần tính  \(\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}\).

Chọn B.

Câu 2 (TH):

Phương pháp:

Hàm phân thức, hàm đa thức liên tục trên các tập xác định của chúng.

Cách giải:

Hàm số \(y = \frac{{3x - 5}}{{x + 3}}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)

\( \Rightarrow \) Hàm số không liên tục trên \(\mathbb{R}\).

Vậy khẳng định B sai.

Chọn B.

Câu 3 (TH):

Phương pháp:

Xác định đoạn vuông góc chung của hai đường \(AD\) và \(HF\).

Cách giải:

Ta có \(HD \bot \left( {ABCD} \right) \Rightarrow HD \bot AB\)

\(HD \bot \left( {EFGH} \right) \Rightarrow HD \bot HF\)

\( \Rightarrow HD\) là đoạn vuông góc chung của \(AD\) và \(HF\)\( \Rightarrow d\left( {AD;HF} \right) = HD = 5\).

Chọn B.

Câu 4 (NB):

Phương pháp:

Sử dụng công thức \(\left( {\sin x} \right)' = \cos x\).

Cách giải:

Ta có : \(y' = 2\cos x\).

Chọn C.

Câu 5 (TH):

Phương pháp:

Tính giới hạn từng đáp án và kết luận.

Cách giải:

Ta có: \(\lim \,( - 3{n^4} + 3)\)\( = \lim {n^4}\left( { - 3 + \frac{3}{{{n^4}}}} \right) =  - \infty \)

Đáp án A đúng.

Chọn A.

Câu 6 (NB):

Phương pháp:

Sử dụng công thức vi phân \(y = f\left( x \right) \Rightarrow dy = f'\left( x \right)dx\).

Cách giải:

\(dy = \left( {{x^3} - 3x + 1} \right)'dx\)\( = \left( {3{x^2} - 3} \right)dx\).

Chọn C.

Câu 7 (NB):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\)\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Cách giải:

Ta có: \(\mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} + 3x - 1}}{{x + 1}}\)\( = \frac{{{{2.1}^2} + 3.1 - 1}}{{1 + 1}} = \frac{4}{2} = 2\).

Chọn D.

Câu 8 (TH):

Phương pháp:

\(\left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\).

Cách giải:

Ta có \(\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\end{array} \right. \Rightarrow OC \bot \left( {OAB} \right)\).

Mà \(\left\{ \begin{array}{l}OC \subset \left( {OAC} \right)\\OC \subset \left( {OBC} \right)\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}\left( {OAB} \right) \bot \left( {OAC} \right)\\\left( {OAB} \right) \bot \left( {OBC} \right)\end{array} \right.\)

\( \Rightarrow B,D\) đúng.

Ta có \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right)\).

Mà \(OA \subset \left( {OAC} \right)\)\( \Rightarrow \left( {OAC} \right) \bot \left( {OBC} \right)\) \( \Rightarrow C\) đúng.

Chọn A.

Câu 9 (TH):

Phương pháp:

Hình hộp chữ nhật là lăng trụ đứng có đáy là hình chữ nhật.

Cách giải:

Ta có \(HE \bot \left( {MNEF} \right) \Rightarrow \left\{ \begin{array}{l}HE \bot NF\\HE \bot MN\end{array} \right.\)

\(HE \bot \left( {GHPQ} \right) \Rightarrow HE \bot GP\).

Vậy chỉ có khẳng định D sai.

Chọn D.

Câu 10 (NB):

Phương pháp:

Sử dụng công thức tính đạo hàm \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne  - 1} \right)\).

Cách giải:

Ta có \(f'\left( x \right) = 3{x^2} - 6x\)\( \Rightarrow f''\left( x \right) = 6x - 6\)  

Chọn A.

Câu 11 (NB):

Phương pháp:

Sử dụng công thức tính đạo hàm \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne  - 1} \right)\).

Cách giải:

\(f'\left( x \right) = 3.3{x^2} = 9{x^2}\).

Chọn D.

Câu 12 (TH):

Phương pháp:

\(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

Cách giải:

Ta có \(\left\{ \begin{array}{l}B'C' \bot BB'\\B'C' \bot A'B'\end{array} \right.\)\( \Rightarrow B'C' \bot \left( {BB'A'} \right)\)

\( \Rightarrow A\) đúng.

Chọn A.

Câu 13 (TH):

Phương pháp:

Sử dụng công thức hình bình hành.

Cách giải:

\(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AE} \)\( = \overrightarrow {AC}  + \overrightarrow {AE}  = \overrightarrow {AG} \).

Chọn A.

Câu 14 (NB):

Cách giải:

Chọn B.

Câu 15 (TH):

Phương pháp:

Sử dụng công thức vi phân \(y = f\left( x \right)\)\( \Rightarrow dy = f'\left( x \right)dx\).

Cách giải:

\(dy = \left( {\cos 2x + \cot x} \right)'dx\)\( = \left( { - 2\sin 2x - \frac{1}{{{{\sin }^2}x}}} \right)dx\) .

Chọn D.

Câu 16 (TH):

Phương pháp:

Chia cả tử và mẫu cho n với số mũ lớn nhất.

Cách giải:

\(\lim \frac{{ - 2{n^2} - 1}}{{5{n^2} - 8}}\)\( = \lim \frac{{ - 2 - \frac{1}{{{n^2}}}}}{{5 - \frac{8}{{{n^2}}}}} =  - \frac{2}{5}\)

\( \Rightarrow \) Đáp án C đúng.

Chọn C.

Câu 17 (TH):

Phương pháp:

Phân tích, rút gọn, khử dạng \(\frac{0}{0}\).

Cách giải:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 3} \frac{{{x^2} + x - 12}}{{x - 3}}\\ = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {x - 3} \right)\left( {x + 4} \right)}}{{x - 3}}\\ = \mathop {\lim }\limits_{x \to 3} \left( {x + 4} \right) = 7\end{array}\).

Chọn C.

Câu 18:

Cách giải:

Khẳng định sai là B.

Chọn B.

Câu 19 (TH):

Cách giải:

Hai mặt phẳng cắt nhau thì không vuông góc là khẳng định sai.

Chọn B.

Câu 20 (TH):

Phương pháp:

Sử dụng công thức tính đạo hàm \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\,\,\left( {u \ne  - 1} \right)\).

Cách giải:

Ta có

\(\begin{array}{l}f'\left( x \right) = 12{\left( {2x + 1} \right)^{11}}\left( {2x + 1} \right)'\\ = 24{\left( {2x + 1} \right)^{11}}\\f''\left( x \right) = 24.11{\left( {2x + 1} \right)^{10}}.\left( {2x + 1} \right)'\\ = 528{\left( {2x + 1} \right)^{10}}\\ \Rightarrow f''\left( 0 \right) = {528.1^{10}} = 528\end{array}\)

Chọn B.

Câu 21 (TH):

Phương pháp:

Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(f'\left( {{x_0}} \right)\).

Cách giải:

TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\} \Rightarrow {x_0} = 0 \in D\).

Ta có: \(y' = \frac{{1 + 1}}{{{{\left( {x + 1} \right)}^2}}} = \frac{2}{{{{\left( {x + 1} \right)}^2}}}\).

\( \Rightarrow \) Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) tại điểm có hoành độ \({x_0} = 0\) là: \(k = \frac{2}{{{{\left( {0 + 1} \right)}^2}}} = 2\).

Chọn D.

Chú ý: Sử dụng công thức tính nhanh đạo hàm \(\left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\).

Câu 22 (TH):

Phương pháp:

Số gia \(\Delta y\) của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) ứng với số gia \(\Delta x\) là \(\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\). 

Cách giải:

Đặt \(y = {x^2} = f\left( x \right)\) ta có:

\(\begin{array}{l}\Delta y = f\left( {{x_0} + \Delta x} \right) - f\left( {{x_0}} \right)\\ = f\left( {3 - 1} \right) - f\left( 3 \right)\\ = f\left( 2 \right) - f\left( 3 \right) = {2^2} - {3^2}\\ =  - 5\end{array}\)

Chọn C.

Câu 23 (VD): 

Phương pháp:

Nhân chia cho biểu thức liên hợp của \(\sqrt {{x^2} + 4}  + x\).

Cách giải:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 4}  + x} \right)\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\left( {\sqrt {{x^2} + 4}  + x} \right)\left( {\sqrt {{x^2} + 4}  - x} \right)}}{{\sqrt {{x^2} + 4}  - x}}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{{x^2} + 4 - {x^2}}}{{\sqrt {{x^2} + 4}  - x}}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{4}{{\sqrt {{x^2} + 4}  - x}}\\ = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\frac{4}{x}}}{{ - \sqrt {1 + \frac{4}{{{x^2}}}}  - 1}}\\ = \frac{0}{{ - 2}} = 0\end{array}\)

Chọn A.

Câu 24 (VD):

Phương pháp:

Sử dụng công thức đổi đỉnh tính khoảng cách.

Cách giải:

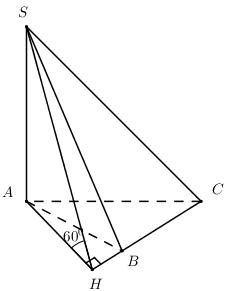
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

Gọi \(M\) là trung điểm của \(CD\) ta có \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right)\).

Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có

\(\left\{ \begin{array}{l}OH \bot SM\\OH \bot CD\end{array} \right. \Rightarrow OH \bot \left( {SCD} \right)\)\( \Rightarrow d\left( {O;\left( {SCD} \right)} \right) = OH\).

Ta có \(BO \cap \left( {SCD} \right) = D\)\( \Rightarrow \frac{{d\left( {B;\left( {SCD} \right)} \right)}}{{d\left( {O;\left( {SCD} \right)} \right)}} = \frac{{BD}}{{OD}} = 2\).

\( \Rightarrow d\left( {B;\left( {SCD} \right)} \right)\)\( = 2d\left( {O;\left( {SCD} \right)} \right) = 2OH\).

Ta có \(OM\) là đường trung bình của \(\Delta ACD\)

\( \Rightarrow OM = \frac{1}{2}AD = 3\,\,\left( {cm} \right)\).

Trong \(\Delta SOC\) có: \(SO = \sqrt {S{C^2} - O{C^2}} \)\( = \sqrt {{6^2} - {{\left( {\frac{{6\sqrt 2 }}{2}} \right)}^2}}  = 3\sqrt 2 \) (cm).

Áp dụng hệ thức lượng trong tam giác vuông \(SOM\) ta có: \(OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + O{M^2}} }}\)\( = \frac{{3\sqrt 2 .3}}{{\sqrt {18 + 9} }} = \sqrt 6 \).

Vậy \(d\left( {B;\left( {SCD} \right)} \right) = 2\sqrt 6 \,\,\left( {cm} \right)\).

Chọn C.

Câu 25 (VD):

Phương pháp:

Sử dụng quy tắc tính đạo hàm \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).

Cách giải:

Ta có

\(\begin{array}{l}y' = \frac{{2x\left( {x + 1} \right) - \left( {{x^2} + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{2{x^2} + 2x - {x^2} - 3}}{{{{\left( {x + 1} \right)}^2}}}\\ = \frac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}}\end{array}\)

\(\begin{array}{l}y' > 0 \Leftrightarrow \frac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}} > 0\\ \Leftrightarrow {x^2} + 2x - 3 > 0\\ \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\end{array}\).

Chọn A.

Câu 26 (VD):

Phương pháp:

Đáp án A: Chia cả tử và mẫu cho \({4^n}\).

Đáp án B: Chia cả tử và mẫu cho \({n^2}\).

Đáp án C: Chia cả tử và mẫu cho \({8^n}\).

Đáp án D: Chia cả tử và mẫu cho \(n\).

Cách giải:

\(\begin{array}{l} + )\,\,\lim \frac{{{{5.4}^n} + {{7.2}^n} - {3^n}}}{{{{4.4}^n} - {{2.3}^n}}}\\ = \lim \frac{{5 + 7.{{\left( {\frac{2}{4}} \right)}^n} - {{\left( {\frac{3}{4}} \right)}^n}}}{{4 - 2{{\left( {\frac{3}{4}} \right)}^n}}} = \frac{5}{4}\\ + )\,\,\lim \frac{{\sqrt {9{n^2} + 4}  - n}}{{{n^2}}}\\ = \lim \frac{{\sqrt {\frac{9}{{{n^2}}} + \frac{4}{{{n^4}}}}  - \frac{1}{n}}}{1} = 0\\ + )\,\,\lim \frac{{{3^n} + {{4.5}^n} - {8^n}}}{{{{3.8}^n} + {{2.6}^n}}}\\ = \lim \frac{{{{\left( {\frac{3}{8}} \right)}^n} + 4{{\left( {\frac{5}{8}} \right)}^n} - 1}}{{3 + 2{{\left( {\frac{6}{8}} \right)}^n}}}\\ =  - \frac{1}{3}\\ + )\,\,\lim \frac{{\sqrt {{n^2} + 4}  + n}}{n}\\ = \lim \frac{{\sqrt {1 + \frac{4}{{{n^2}}}}  + 1}}{1} = 1\end{array}\)

Chọn D.

Câu 27 (VD):

Phương pháp:

Sử dụng công thức

\(\begin{array}{l}\left( {\cos u} \right)' =  - u'.\sin u\\\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}\end{array}\).

Cách giải:

\(\begin{array}{l}y' =  - \left( {\sqrt {2{x^2} - x + 7} } \right)'sin\sqrt {2{x^2} - x + 7} \\y' =  - \frac{{\left( {2{x^2} - x + 7} \right)'}}{{2\sqrt {2{x^2} - x + 7} }}sin\sqrt {2{x^2} - x + 7} \\y' = \frac{{ - 4x + 1}}{{2\sqrt {2{x^2} - x + 7} }}sin\sqrt {2{x^2} - x + 7} \\y' = \frac{{\left( {1 - 4x} \right)sin\sqrt {2{x^2} - x + 7} }}{{2\sqrt {2{x^2} - x + 7} }}\end{array}\)

Chọn C.

Câu 28 (VD):

Phương pháp:

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

Cách giải:

Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \)\(\Rightarrow SA \bot \left( {ABC} \right)\).

Xét tam giác \(ABC\) ta có

\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}}\)\( = \frac{{{4^2} + {6^2} - {8^2}}}{{2.4.6}} =  - \frac{1}{4} < 0\)

\( \Rightarrow \widehat B > {90^0}\)

Trong \(\left( {ABC} \right)\) dựng \(AH \bot BC\,\,\left( {H \in BC} \right)\) ta có:

\(\left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right)\)\( \Rightarrow BC \bot SH\).

\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SH \bot \left( {ABC} \right)\\\left( {ABC} \right) \supset AH \bot \left( {ABC} \right)\end{array} \right.\)

\( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right)\) \( = \angle \left( {SH;AH} \right) = \angle SHA = {60^0}\) .

Xét tam giác vuông \(AHB\) có \(BH = AB.\cos \angle ABH\)\( = 4.\frac{1}{4} = 1\).

\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} \)\( = \sqrt {{4^2} - {1^2}}  = \sqrt {15} \).

Xét tam giác vuông \(SAH\) có : \(SA = AH.\tan {60^0}\)\( = \sqrt {15} .\sqrt 3  = 3\sqrt 5 \).

Chọn D.

Câu 29 (VD):

Phương pháp:

+) Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(k = f'\left( {{x_0}} \right)\).

+) Tiếp tuyến song song với đường thẳng \(\Delta :\,\,12x - y - 2018 = 0\)\( \Leftrightarrow y = 12x - 2018\) \( \Rightarrow k = 12\).

Cách giải:

Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = {\left( {x - 1} \right)^3}\) tại điểm có hoành độ \(x = {x_0}\) là \(k = 3{\left( {{x_0} - 1} \right)^2}\).

Tiếp tuyến song song với đường thẳng \(\Delta :\,\,12x - y - 2018 = 0\)\( \Leftrightarrow y = 12x - 2018\) \( \Rightarrow k = 12\).

\(\begin{array}{l} \Rightarrow 3{\left( {{x_0} - 1} \right)^2} = 12\\ \Leftrightarrow {\left( {{x_0} - 1} \right)^2} = 4\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} - 1 = 2\\{x_0} - 1 =  - 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 3\\{x_0} =  - 1\end{array} \right.\end{array}\).

Với \({x_0} = 3\), phương trình tiếp tuyến cần tìm là : \(y = 12\left( {x - 3} \right) + 8\)\( = 12x - 28\,\,\,\left( {tm} \right)\) .

Với \({x_0} =  - 1\), phương trình tiếp tuyến cần tìm là : \(y = 12\left( {x + 1} \right) - 8\)\( = 12x + 4\,\,\,\left( {tm} \right)\) .

Chọn D.

Câu 30 (VD):

Phương pháp:

Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Cách giải:

Hàm số liên tục trên các khoảng \(\left( { - \infty ;3} \right)\) và \(\left( {3; + \infty } \right)\). Để hàm số liên tục trên \(\mathbb{R}\) thì hàm số phải liên tục tại \(x = 3\).

Ta có

\(\begin{array}{l} + )\,\,\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} 5 = 5\\ + )\,\,\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ - }} \left( {2b{x^2} - 4} \right)\\ = 18b - 4\\ + )\,\,f\left( 3 \right) = 18b - 4\end{array}\)

Hàm số liên tục tại \(x = 3\)\( \Leftrightarrow 18b - 4 = 5 \Leftrightarrow b = \frac{1}{2}\).

Vậy hàm số đã cho liên tục trên \(\mathbb{R}\)\( \Leftrightarrow b = \frac{1}{2}\).

Chọn D.

 

II. PHẦN TỰ LUẬN (4.0 điểm) (Học sinh viết bài làm vào giấy, ghi rõ mã đề)

Bài 1 (TH):

Phương pháp:

a) Chia cả tử và mẫu cho \(n\).

b) Phân tích, rút gọn để khử dạng \(\frac{0}{0}\).

Cách giải:

a) \(\lim \frac{{4n + 9}}{{6n - 7}} = \lim \frac{{4 + \frac{9}{n}}}{{6 - \frac{7}{n}}} = \frac{4}{6} = \frac{2}{3}\).

b) \(\mathop {\lim }\limits_{x \to \, - 2} \frac{{2 - 5x - 3{x^2}}}{{2x + 4}}\)

\(\begin{array}{l} = \mathop {\lim }\limits_{x \to \, - 2} \frac{{\left( {x + 2} \right)\left( {1 - 3x} \right)}}{{2\left( {x + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to \, - 2} \frac{{1 - 3x}}{2} = \frac{7}{2}\end{array}\)

Bài 2 (VD):

Phương pháp:

a) Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne  - 1} \right)\).

b) Sử dụng công thức \(\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}\).

Cách giải:

a) \(y' = 3{x^2} + 8x - 2\)

\( \Rightarrow y'\left( { - 4} \right) = 3.{\left( { - 4} \right)^2} + 8.\left( { - 4} \right) - 2\)\( = 14\).

b)

\(\begin{array}{l}y' = \frac{{\left( {7 + 5{{\cot }^4}{x^4}} \right)'}}{{2\sqrt {7 + 5{{\cot }^4}{x^4}} }}\\ = \frac{{20{{\cot }^3}{x^4}.\left( {\cot {x^4}} \right)'}}{{2\sqrt {7 + 5{{\cot }^4}{x^4}} }}\\ = \frac{{10{{\cot }^3}{x^4}\frac{{ - \left( {{x^4}} \right)'}}{{{{\sin }^2}{x^4}}}}}{{2\sqrt {7 + 5{{\cot }^4}{x^4}} }}\\ = \frac{{ - 20{x^3}{{\cot }^3}{x^4}}}{{{{\sin }^2}{x^4}\sqrt {7 + 5{{\cot }^4}{x^4}} }}\end{array}\)

Bài 3 (VD):

Phương pháp:

+) Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne  - 1} \right)\) tính \(y''\).

+) Bất phương trình \(y'' < 0\) vô nghiệm \( \Leftrightarrow y'' \ge 0\) nghiệm đúng \(\forall x\).

Cách giải:

\(y = \frac{{m-1}}{{12}}{x^4}-\frac{{m + 1}}{3}{x^3}\)\( + \frac{{{\rm{3(}}m - 2)}}{2}{x^2} + 7x + 2020\)

\( \Rightarrow y' = \frac{{\left( {m - 1} \right){x^3}}}{3} - \left( {m + 1} \right){x^2}\)\( + 3\left( {m - 2} \right)x + 7\)  

\(y'' = \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x\)\( + 3\left( {m - 2} \right)\)  

Bất phương trình \(y'' < 0\) vô nghiệm

\( \Leftrightarrow \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x\) \( + 3\left( {m - 2} \right) < 0\) vô nghiệm

\( \Leftrightarrow \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x\)\( + 3\left( {m - 2} \right) \ge 0\) nghiệm đúng \(\forall x\).

TH1: \(m = 0\)

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow  - 2x - 6 \ge 0\\ \Leftrightarrow x \le  - 3 \Rightarrow m = 0\,\,\left( {ktm} \right)\end{array}\)

TH2: \(m \ne 0\)

\( \Rightarrow \left( * \right) \Leftrightarrow \left\{ \begin{array}{l}m - 1 > 0\\\Delta ' \le 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m > 1\\{\left( {m + 1} \right)^2} - 3\left( {m - 1} \right)\left( {m - 2} \right) \le 0\end{array} \right.\)  

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m > 1\\{m^2} + 2m + 1 - 3\left( {{m^2} - 3m + 2} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\ - 2{m^2} + 11m - 5 \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\\left[ \begin{array}{l}m \ge 5\\m \le \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \ge 5\end{array}\).

Vậy \(m \ge 5\).

Bài 4 (VD):

Phương pháp:

a) \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \cap \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

b) \(\left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\).

c) Chứng minh \(d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\).

Cách giải:

a) Ta có \(\left\{ \begin{array}{l}CD \bot AD\,\,\left( {gt} \right)\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow CD \bot \left( {SAD} \right)\) .

b) Ta có \(\left\{ \begin{array}{l}BD \bot AC\,\,\left( {gt} \right)\\BD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow BD \bot \left( {SAC} \right)\) .

Mà \(AC \subset \left( {SAC} \right)\)\( \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\) .

c) Ta có \(AB//CD \Rightarrow AB//\left( {SCD} \right)\)\( \Rightarrow d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\) .

Trong \(\left( {SAD} \right)\) kẻ \(AH \bot SD\) ta có:

\(CD \bot \left( {SAD} \right)\,\,\left( {cmt} \right)\)\( \Rightarrow CD \bot AH\) .

Lại có \(AH \bot SD \Rightarrow AH \bot \left( {SCD} \right)\).

\( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AH\).

Áp dụng hệ thức lượng trong tam giác vuông \(SAD\) ta có: \(AH = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }}\)\( = \frac{{a\sqrt 5 .a}}{{\sqrt {5{a^2} + {a^2}} }} = \frac{{a\sqrt {30} }}{6}\) .

Vậy \(d\left( {AB;\left( {SCD} \right)} \right) = \frac{{a\sqrt {30} }}{6}\).

Loigiaihay.com