Đề kiểm tra giữa kì I Toán 7 - Đề số 2 có lời giải chi tiết

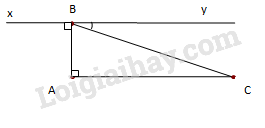
Đề bài

I.Trắc nghiệm: (2điểm) Chọn đáp án đúng

1.  Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \(\frac{1}{{ - 2}}\)

   A.\(\frac{{ - 3}}{5}\);                                  B.\(\frac{7}{{ - 14}}\);                           

    C.\(\frac{{ - 14}}{{ - 28}}\);                                D.\(\frac{7}{{14}}\)

  2.  Kết quả của phép tính \({\left( { - \frac{1}{2}} \right)^3}\) là:

  A.\(\frac{{ - 3}}{6}\);                                  B.\(\frac{1}{8}\);                 

C.\(\frac{{ - 3}}{8}\);                                   D.\(\frac{{ - 1}}{8}\)

  3.   Tỉ lệ thức nào sau đây không thể suy ra từ đẳng thức a.b = c.d

  A. \(\frac{a}{b} = \frac{c}{d}\);                             B. \(\frac{a}{c} = \frac{d}{b}\);         

  C. \(\frac{b}{c} = \frac{d}{a}\);                             D. \(\frac{a}{d} = \frac{c}{b}\).

  4.  Cho 3 đường thẳng \(a\), \(b\), \(c\). Biết \(a\)//\(c\) và \(\left( c \right)\)\( \bot \)\(\left( b \right)\). Khẳng định nào sau đây là đúng:

  A. a\( \bot \)b;                                       

  B. a và b cùng vuông góc với c;

  C. a // b;                                       

  D. a và b cùng song song với c.

II.Tự luận: (8 điểm)

Câu 1: (2 điểm) Thực hiện phép tính:

a) \(\)\( - \frac{{12}}{5}:\left( { - 6} \right)\) ;                        

b) \(\left[ {8.{{\left( {\frac{1}{2}} \right)}^3} + {3^3}} \right]\).\(\frac{1}{9}\)

Câu 2: (1,5 điểm) Tìm x biết:

a)  \(\frac{5}{2}x - \frac{1}{3} = \frac{4}{3}\)           

b)\(\left| {2x + 0,5} \right| = 8,5\)

Câu 3: (1,5 điểm):

Một hộp đựng ba loại bi màu khác nhau. Số lượng loại bi màu xanh, bi màu

vàng và bi màu đỏ tỉ lệ với các số 5, 7, 9. Tính số bi mỗi loại, biết số bi màu

xanh ít hơn số bi màu vàng 4 viên.

Câu 4: (2 điểm): :  Cho tam giác ABC có \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A}  = {90^0}\). Qua đỉnh B của tam giác kẻ

đường thẳng xy vuông góc với cạnh AB ( AC, By thuộc cùng một nửa mặt

phẳng có bờ là đường thẳng chứa cạnh AB).

   a) Chứng minh xy // AC.

   b) Biết góc \(C\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y = {35^0}\). Tính số đo các góc còn lại của tam giác ABC.

Câu 5: (1 điểm)

 Tìm x, y biết:  \({\left( {\frac{1}{3} - 2x} \right)^{102}} + {\left( {3y - x} \right)^{104}} = 0\)

Lời giải chi tiết

I.Trắc nghiệm

II.Tự luận

Câu 1:

a) \( - \frac{{12}}{5}:\left( { - 6} \right)\)=\( - \frac{{12}}{5}.\left( {\frac{1}{{ - 6}}} \right) = \frac{2}{5}\)

b) \(\left[ {8.{{\left( {\frac{1}{2}} \right)}^3} + {3^3}} \right]\).\(\frac{1}{9}\) = \(\left( {8.\frac{1}{8} + 27} \right).\frac{1}{9}\)

=\(\left( {1 + 27} \right).\frac{1}{9} = \frac{{28}}{9}\)

Câu 2:

a) \(\frac{5}{2}x - \frac{1}{3} = \frac{4}{3}\)   \( \Rightarrow \frac{5}{2}x = \frac{4}{3} + \frac{1}{3}\)              

\(\frac{5}{2}x = \frac{5}{3} \Rightarrow x = \frac{5}{3}:\frac{5}{2} = \frac{2}{3}\)

Vậy \(x = \frac{2}{3}\)

b) \(\left| {2x + 0,5} \right| = 8,5\)

\( \Rightarrow 2x + 0,5 = 8,5\) hoặc \(2x + 0,5 =  - 8,5\)

\( \Rightarrow 2x = 8\) hoặc \(2x =  - 9\)

\( \Rightarrow x = 4\) hoặc \(x = \frac{{ - 9}}{2}\)

    Vậy \(x = 4\) hoặc \(x = \frac{{ - 9}}{2}\).

Câu 3: Gọi số bi màu xanh, vàng, đỏ lần lượt là x, y, z \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\) (viên)

     \( \Rightarrow \)\(\frac{x}{5} = \frac{y}{7} = \frac{z}{9}\) và \(y - x = 4\)

           Từ đó  \(\frac{x}{5} = \frac{y}{7} = \frac{z}{9} = \frac{{y - x}}{{7 - 5}} = \frac{4}{2} = 2\)

tìm được \(x = 2.5= 10;y = 2.7= 14;z = 2.9= 18.\)

KL: Vậy số bi màu xanh, vàng, đỏ lần lượt là 10 viên, 14 viên, 18 viên

Câu 4:

a) - Ta có \(\Delta ABC\)vuông tại A \( \Rightarrow \)\(AC \bot AB\) (1)

- \(xy \bot AB\) (gt)  (2)

- Từ (1) và (2) \( \Rightarrow \)xy // AC

b) Có \(xy \bot AB\) (gt)  \( \Rightarrow \)góc \(A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y = {90^0}\)

Mặt khác \(A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y = A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} C + C\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y\)

                       \( \Rightarrow A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} C = A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y - C\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over B} y\) \( = {90^0} - {35^0} = {55^0}\)

- Dựa vào tính chất tổng ba góc trong tam giác ABC hoặc

 từ  xy // AC   tính được góc \(A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over C} B = {35^0}\)

   Vậy \(A\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over C} B = {35^0}\)

Câu 5:

Vì \({\left( {\frac{1}{3} - 2x} \right)^{102}} \ge 0\) với \(\forall x\); \({\left( {3y - x} \right)^{104}} \ge 0\) với \(\forall x,y\).

 \( \Rightarrow \)\({\left( {\frac{1}{3} - 2x} \right)^{102}} + {\left( {3y - x} \right)^{104}} = 0\) \(\Leftrightarrow \) \({\left( {\frac{1}{3} - 2x} \right)^{102}} = 0\) và \({\left( {3y - x} \right)^{104}} = 0\)

\(\Leftrightarrow \) \(\frac{1}{3} - 2x = 0\) và \(3y - x = 0\)

\(\Leftrightarrow \) \(x = \frac{1}{6};y = \frac{1}{{18}}\).

Vậy \(x = \frac{1}{6};y = \frac{1}{{18}}\)

 Loigiaihay.com