Đề kiểm tra giữa kì I Toán 7 - Đề số 1 có lời giải chi tiết

Đề bài

I ) TRẮC NGHIỆM : ( 2điểm )

Hãy khoanh tròn vào chữ cái đứng trước câu trả lời em cho là đúng:

Câu 1: Nếu \(\sqrt 4  =\sqrt x \) thì x bằng

    A.       2                   B:    4                             C: 16                        D:  8

Câu 2: Cho số hữu tỉ  \(\frac{a}{b}\)

A.  \(\frac{a}{b}\) là số dương nếu a âm và b âm.                      C.  \(\frac{a}{b}\)  là số dương nếu b dương

B.   \(\frac{a}{b}\) là số dương nếu a dương                               D. \(\frac{a}{b}\) là số âm nếu a âm

Câu 3: Cho \(\frac{{3x - y}}{{x + y}} = \frac{3}{4}\)  khi đó  \(\frac{x}{y}\)bằng

 A. \(\frac{3}{4}\)           B.  \(\frac{9}{7}\)            C. \(\frac{7}{9}\)          D. \(\frac{6}{4}\)

Câu 4:  Từ \(\frac{5}{4} - x = \frac{{ - 3}}{2}\) suy ra \(x\)bằng :

A.\(\frac{{ - 1}}{4}\)      B.\(\frac{{11}}{4}\)     C. \(\frac{{ - 11}}{4}\)      D. \(\frac{1}{4}\)

Câu 5: Đẳng thức được suy ra từ tỷ lệ thức \(\frac{m}{n} = \frac{t}{h}\) là:

A.  m . n = t . h             B.  m . t = n . h         C.  m . h = n . t            D. m + h = n + t

Câu 6:  Phân số nào sau đây viết được dưới dạng số thập phân hữu hạn?              

A.    \(\frac{{11}}{{30}}\)                               

B.   \(\frac{{12}}{7}\) 

C. \(\frac{{25}}{{18}}\)                               

D. \( - \frac{8}{{25}}\)

Câu 7:   A. Hai góc bằng nhau thì đối đỉnh.

            B . Hai góc không đối đỉnh thì không bằng nhau.

            C . Hai góc đối đỉnh thì bằng nhau.

            D. Cả ba đáp án trên đều đúng.

Câu 8: Hai tam giác bằng nhau thì.

A.    Ba góc của tam giác này bằng ba góc của tam giác kia.

B.     Ba cạnh của tam giác này bằng ba cạnh của tam giác kia.

C.     Ba đỉnh của tam giác này bằng ba đỉnh của tam giác kia.

D.    Cả ba đáp án trên đều sai.

II. TỰ LUẬN:(8 điểm)

 Bài 1: (1điểm)Tính bằng cách hợp lí (nếu có thể).

a)      \(\frac{{35}}{{17}} - \frac{{84}}{{32}} - \frac{{18}}{{17}} + \frac{{26}}{{16}}\)

b)      \(\sqrt {{3^2} + {4^2}}  - \left( {\sqrt {{3^2}}  + \sqrt {{4^2}} } \right)\)

Bài 2: (2điểm) Tìm x biết  

 a)  \(\left| {x + \frac{3}{4}} \right| = \frac{5}{7}\)                                    

 b)    \( - \frac{5}{7} - x =  - \frac{9}{{10}}\)

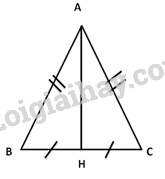
 Bài 3: (1,5 điểm ) Trong đợt trồng cây do nhà trường phát động. Ba lớp 7A; 7B và 7C đã trồng được số cây tỉ lệ với  2; 3; 4.Biết rằng tổng số cây trồng của ba lớp  là 108 cây .Tính số cây mỗi lớp trồng được.

 Bài 4: ( 2,5 điểm) Cho tam giác ABC có AB = AC .Gọi H là trung điểm của cạnh BC.

   Chứng minh.

a)   \(\Delta AHB = \Delta AHC.\)

b)   AH là tia phân giác của góc BAC.

c)   AH vuông góc với BC.

 Bài 5: (1điểm):

 Cho \(N\, = \,\frac{9}{{\sqrt x \, - \,5}}\) (với \(x\, \ge \,0\)). Tìm số nguyên x để N có giá trị nguyên.   

Lời giải chi tiết

I/ TRẮC NGHIỆM  (2 điểm) Mỗi câu đúng cho 0,25đ

II/ TỰ LUẬN  (8 điểm)

 Câu 1:

Thực hiện phép tính:

 a. \(\frac{{35}}{{17}} - \frac{{84}}{{32}} - \frac{{18}}{{17}} + \frac{{26}}{{16}}\) =  \(\left( {} \right.\frac{{35}}{{17}} - \frac{{18}}{{17}}\left. {} \right) - \left( {} \right.\frac{{84}}{{32}} - \frac{{26}}{{16}}\left. {} \right) = 1 - 1 = 0\)

b)   \(\sqrt {{3^2} + {4^2}}  - \left( {} \right.\sqrt {{3^2}}  + \sqrt {{4^2}\left. {} \right)} \)= \(\sqrt {25}  - \left( 3 \right. + \left. 4 \right) = 5 - 7 =  - 2\)

Câu 2:

a) \(\left| {x + \frac{3}{4}} \right| = \frac{5}{7}\)

\(\begin{array}{l}\left[ {_{x + \frac{3}{4} =  - \frac{5}{7}}^{x + \frac{3}{4} = \frac{5}{7}} \Rightarrow \left[ {_{x =  - 1\frac{{13}}{{28}}}^{x =  - \frac{1}{{28}}}} \right.} \right.\\\end{array}\)

b) \( - \frac{5}{7} - x =  - \frac{9}{{10}}\)

             \(x =  - \frac{5}{7} - ( - \frac{9}{{10}})\)

            \(\begin{array}{l}x =  - \frac{{50}}{{70}} + \frac{{63}}{{70}}\\x = \frac{{13}}{{70}}\end{array}\)

Câu 3:

Gọi số cây trồng đ­ược của lớp 7A ,7B,7C là x ,y,z (cây) (x,y,z\( \in \) Z, x,y,z > 0)

Ta có:  \(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\) và  x + y + z = 108 .

Theo tính chất dãy tỉ số bằng nhau,  ta có :\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{{x + y + z}}{{2 + 3 + 4}} = \frac{{108}}{9} = 12\)    

                \(\frac{x}{2} = 12 \Rightarrow x = 24\)     ;      \(\frac{y}{3} = 12 \Rightarrow y = 36\)   ;        \(\frac{z}{4} = 12 \Rightarrow z = 48\)     (tmđk)                                     

Vậy số cây của lớp 7A trồng đ­ược là 24 cây

            số cây của lớp 7B trồng đ­ược là 36 cây    

            số cây của lớp 7C trồng đ­ược là 48 cây    

Câu 4:

a) Xét \(\Delta AHB\) và \(\Delta AHC\) có:

AH chung

AB=AC(gt)

BH=CH (H là trung điểm của BC)

=>\(\Delta AHB\)=\(\Delta AHC\)(c.c.c)(1)

b)

Do (1) nên \(\widehat {BAH} = \widehat {CAH}\)

Suy ra AH là phân giác của góc BAC

c)

Do (1) nên\(\widehat {AHB} = \widehat {AHC}\) mà\(\widehat {AHB} + \widehat {AHC} = {180^0}\)

Suy ra \(\widehat {AHB} = \widehat {AHC} = {90^0}\)

\( \Rightarrow AH \bot BC\)

Câu 5:

 Cho \(N\, = \,\frac{9}{{\sqrt x \, - \,5}}\) (với \(x\, \ge \,0\)). Tìm số nguyên x để N có giá trị nguyên.  

Để N có giá trị nguyên thì \(\,\frac{9}{{\sqrt x \, - \,5}}\) phải là một số nguyên. Để \(\sqrt x \, - \,5\) là số nguyên thì \(\sqrt x \) phải là số nguyên (nếu x là số chính phương) => 9 phải chia hết cho \(\sqrt x \, - \,5\)  => \(\sqrt x \, - \,5\) \( \in \)Ư(9)             

Mà Ư(9) = {1;-1 ; 3; -3; 9; -9}                                                                                           

 Ta có bảng giá trị của x sau

 Vậy x \( \in \) {36; 64; 196 ; 16; 4 } thì biểu thức N có giá trị nguyên.                                     

                                                                                                                                    Loigiaihay.com