Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 2 - Hình học 9

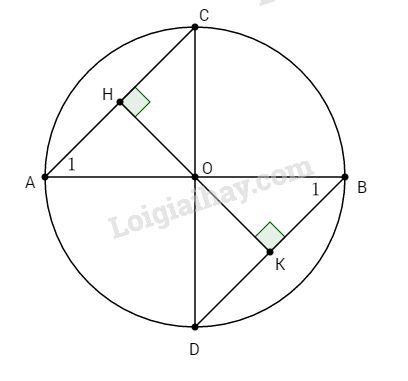
Đề bài

Cho đường tròn tâm O, đường kính AB. Từ A và B kẻ hai dây cung AC và BD song song với nhau.

a. Chứng minh : \(AC = BD\). 

b. Chứng minh rằng ba điểm C, O, D thẳng hàng.

Lời giải chi tiết

a. Kẻ \(OH ⊥ AC\), vì AC // BD (gt) nên

\(OH ⊥ BD\) tại K 

Xét hai tam giác vuông OHA và OKB có:

\({\widehat A_1} = {\widehat B_1}\) (so le trong)

\(OA = OB (=R)\)

Do đó ∆OHA = ∆OKB (cạnh huyền – góc nhọn)

\(⇒ AH = BK ⇒ AC = BD\)

b. Xét ∆OHC và ∆OKD có: \(OH = OK\) (cmt)

\(\widehat {OHC} = \widehat {OKD}\,\left( { = 90^\circ } \right)\)

\(HC = KD\)

Vậy \(∆OHC = ∆OKD\) (c.g.c) \( \Rightarrow \widehat {HOC} = \widehat {KOD}\)

Do đó ba điểm C, O, D thẳng hàng.

Loigiaihay.com