Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 2 - Hình học 9

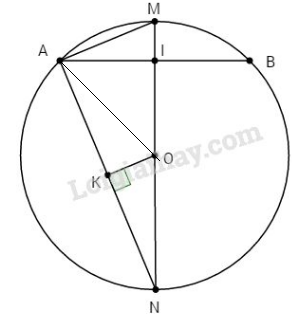
Đề bài

Cho đường tròn (O; R) và một dây cung AB. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M.

a. Cho R = 5cm, AB = 6cm. Tính độ dài dây cung MA. 

b. Cho MN là đường kính của đường tròn (O; R), biết AN = 10cm và dây AB = 12cm. Tính bán kính R.

Lời giải chi tiết

a. Ta có: I là trung điểm của dây AB (gt) nên \(OI \bot AB\) tại I (định lí đường kính dây cung)

Và \( IA = IB = {{AB} \over 2} = {6 \over 2} = 3\,\left( {cm} \right)\) 

Trong tam giác vuông AIO ta có:

\(OI = \sqrt {A{O^2} - A{I^2}}  = \sqrt {{5^2} - {3^2}}  \)\(\;= 4\,\left( {cm} \right)\) (định lí Pi-ta-go)

\(⇒ IM = OM – OI = 5 – 4 = 1 (cm)\)

Xét tam giác vuông AIM lại có:

\(AM = \sqrt {A{I^2} + I{M^2}}  = \sqrt {{3^2} + {1^2}}  \)\(\;= \sqrt {10} \,\left( {cm} \right)\) (định lí Pi-ta-go)

b. Chứng minh như trên ta có:

\(IA = IB = {{AB} \over 2} = {{12} \over 2} = 6\left( {cm} \right)\)

Xét tam giác vuông AIN, ta có:

\(NI = \sqrt {A{N^2} - A{I^2}}  = \sqrt {{{10}^2} - {6^2}}  \)\(\;= 8\,\left( {cm} \right)\)

Kẻ OK ⊥ AN, ta có: \(KA = KN = {{AN} \over 2} = {{10} \over 2} = 5\,\left( {cm} \right)\)

Ta có các tam giác vuông AIN và OKN đồng dạng (g.g) (do có góc N chung và \(\widehat I = \widehat K = {90^0}\))

\( \Rightarrow {{NO} \over {NA}} = {{NK} \over {NI}}\)

\(\Rightarrow NO = {{NA.NK} \over {NI}} = {{10.5} \over 8} = 6,25\,\left( {cm} \right)\)

Vậy \(R = 6,25 (cm).\)

Loigiaihay.com