Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 3 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 3 - Hình học 9 Quảng cáo
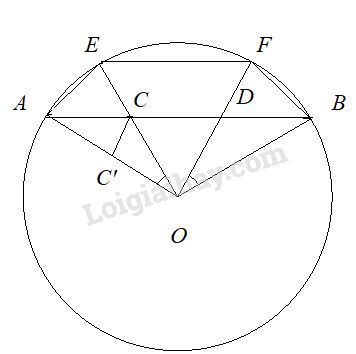
Đề bài Trên dây cung AB của một đường tròn (O), có hai điểm C và D chia dây này ba đoạn bằng nhau: \(AC = CD = DB.\) Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F. Chứng minh rằng các điểm E và F chia cung nhỏ AB thành ba cung : \(\overparen{AE}, \overparen{ EF}, \overparen{FB}\) thỏa mãn điều kiện: \(\overparen{AE} = \overparen{FB}<\overparen{EF}\) Phương pháp giải - Xem chi tiết Chứng minh: \(∆AOC = ∆BOD\) (c.g.c) Và sử dụng + Đường trung bình của tam giác bằng nửa cạnh đáy +Mối liên hệ giữa góc ở tâm và cung bị chắn Lời giải chi tiết
\(∆AOB\) cân (\(OA = OB\)) \( \Rightarrow \widehat {OAB} = \widehat {OBA}\) \( AO = BO\) (gt) \( AC = DB\) (gt) Vậy \(∆AOC = ∆BOD\) (c.g.c) \( \Rightarrow \widehat {AOC} = \widehat {BOD}\) và \(OC = OD\) \( \Rightarrow \overparen{AE} = \overparen{BF}\) Vì D nằm trong đường tròn \( \Rightarrow OA > OD\) Từ C vẽ CC’ // OD. Khi đó CC’ là đường trung bình của ∆AOD \( \Rightarrow CC' = \dfrac{{OD} }{ 2}\) và \(C'O = \dfrac{{AO}}{2}\) \(\widehat {C'CO} = \widehat {COD}\) (so le trong) Ta có: \(CC’ < C’O \Rightarrow \widehat {AOC} < \widehat {C'CO}\) hay \(\widehat {AOC} < \widehat {COD}\) \( \Rightarrow \overparen{AE}<\overparen{EF}\) Loigiaihay.com
|




















Danh sách bình luận