Đề kiểm tra 15 phút - Đề số 2 - Bài 8 - Chương 3 - Hình học 9

Đề bài

Cho đường tròn (O; R). Vẽ tam giác đều nội tiếp và hãy tính cạnh của tam giác theo R.

Lời giải chi tiết

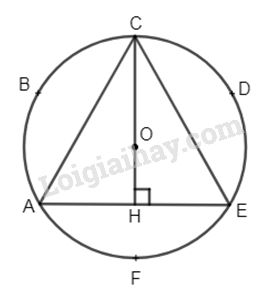
Trên đường tròn (O; R) lấy lần lượt các dây cung \(AB= BC = CD = DE = EF = FA\)\(\, (=R)\)

Nối A với C, C với E, E với A, ta được \(AC = CE = EA\).

Do đó \(∆ACE\) đều.

Ta đã biết : Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm tam giác. Ta có :

\(CH = CO + OH = R + \dfrac{R }{ 2}\) ( tính chất trọng tâm)

\(\;\;\;\;\;\;\; = \dfrac{{3R} }{ 2}\)

∆AHC vuông ta có :

\(AH = CH.\cot A = \dfrac{{3R} }{ 2}.\cot 60^\circ  \)\(\,= \dfrac{{3R} }{2}.\dfrac{1}{ {\sqrt 3 }} = \dfrac{{R\sqrt 3 } }{ 2}\)

\( \Rightarrow AE = R\sqrt 3 .\)      

Vậy cạnh của tam giác đều nội tiếp đường tròn (O; R) là \(R\sqrt 3 .\)

Loigiaihay.com