Đề kiểm tra 15 phút - Đề số 5 - Bài 8 - Chương 3 - Hình học 9

Đề bài

Tính cạnh bát giác đều nội tiếp trong đường tròn (O; R).

Lời giải chi tiết

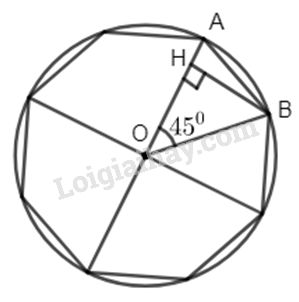
Gọi cạnh của hình bát giác đều là AB.

Kẻ \(BH \bot AO\). Ta có ∆BHO vuông cân \( \Rightarrow  BH = OH.\)

Đặt \(BH = OH = x\). Theo định lí Py-ta-go :

\({x^2} + {x^2} = {R^2} \Rightarrow 2{x^2} = {R^2}\)

\(\Rightarrow {x^2} = \dfrac{{{R^2}}}{ 2}\)

\( \Rightarrow x = \dfrac{{R\sqrt 2 } }{ 2}\)

Hay \(BH = OH =\dfrac {{R\sqrt 2 }}{2}\)

Do đó \(AH = R - OH = R - \dfrac{{R\sqrt 2 } }{2}\)\(\, = R\left( {\dfrac{{2 - \sqrt 2 } }{2}} \right)\)

Xét tam giác vuông AHB có :

\(A{B^2} = A{H^2} + H{B^2}\)

\(\;\;\;\;\;\;\;\;= {\left[ {R\left( {\dfrac{{2 - \sqrt 2 } }{ 2}} \right)} \right]^2} + {\left( {\dfrac{{R\sqrt 2 } }{ 2}} \right)^2}\)

\( \;\;\;\;\;\;\;\;=\dfrac {{{R^2}} }{ 4}\left( {4 - 4\sqrt 2  + 2} \right) + \dfrac{{2{R^2}} }{ 4}\)

\(\;\;\;\;\;\;\;\;=\dfrac {{{R^2}}}{ 4}\left( {4 - 4\sqrt 2  + 2 + 2} \right)\)

\(\;\;\;\;\;\;\;\; =\dfrac {{{R^2}}}{ 4}.4\left( {2 - \sqrt 2 } \right) \)

\(\;\;\;\;\;\;\;\;= {R^2}\left( {2 - \sqrt 2 } \right)\)

\( \Rightarrow AB = R\sqrt {2 - \sqrt 2 } \)

Vậy cạnh bát giác đều nội tiếp (O; R) là \(R\sqrt {2 - \sqrt 2 } .\)

 Loigiaihay.com