Đề kiểm tra 15 phút - Đề số 16 - Bài 4, 5 - Chương 1 - Hình học 8

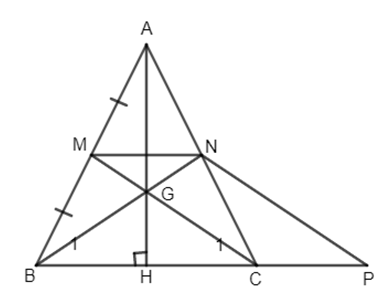
Đề bài

Cho tam giác ABC cân tại A, đường cao AH. Gọi M là trung điểm của AB. G là trung điểm của AH và CM, BG cắt cạnh AC tại N. 

a) Chứng minh rằng BMNC là hình thang cân.

b) Đường thẳng qua N và song song với MC cắt đường thẳng BC tại P. Chứng minh rằng tam giác BNP cân.

c) Chứng minh rằng \(9M{N^2} = P{B^2}.\)

Lời giải chi tiết

a) \(\Delta ABC\) cân tại A nên đường cao AH đồng thời là đường trung tuyến.

M là trung điểm của AB (gt) \( \Rightarrow CM\) là trung tuyến của \(\Delta ABC.\)

G là giao điểm của hai đường trung tuyến AH và CM nên G là trọng tâm của \(\Delta ABC\)

\( \Rightarrow BG\) là trung tuyến thứ ba nên N là trung điểm của AC.

Ta có \(MA = MB = \dfrac{1 }{ 2}AB,\) \(NA = NC = \dfrac{1 }{2}AC\) mà \(AB = AC\) (do \(\Delta ABC\) cân tại A)

\( \Rightarrow MA = MB = NA = NC\) hay \(\Delta AMN\) cân tại A

\( \Rightarrow \widehat {AMN} = \widehat {ANM} = \dfrac{{{{180}^ \circ } - \widehat A}}{ 2}(1)\)

\(\Delta ABC\) cân tại A (gt)

\( \Rightarrow \widehat {ABC} = \widehat {ACB} = \dfrac{{{{180}^ \circ } - \widehat A} }{ 2}\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow \widehat {AMN} = \widehat {ABC}\)

\( \Rightarrow MN// BC\) (cặp góc đồng vị bằng nhau)

Do đó BMNC là hình thang. Lại có \(\widehat B = \widehat C\) nên BMNC là hình thang cân.

b) Xét \(\Delta BGC\) có GH là đường cao đồng thời là trung tuyến (cmt) nên \(\Delta BGC\) cân tại G \( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\) mà \(NP//MC\left( {gt} \right)\)

\(\Rightarrow \widehat {{C_1}} = \widehat P\) (cặp góc đồng vị) \( \Rightarrow \widehat {{B_1}} = \widehat P\) hay \(\Delta BNP\) cân tại N.

c) Ta có MNPC là hình thang (do MN//PC) có hai cạnh bên \(MC//NP\) nên MN = CP.

Lại có \(MN = \dfrac{1 }{ 2}BC\) (MN là đường trung bình của \(\Delta ABC\) )

\( \Rightarrow MN = \dfrac{1 }{3}BP \Rightarrow M{N^2} = \dfrac{1 }{ 9}B{P^2}\)

\(\Rightarrow 9M{N^2} = B{P^2}.\)

Loigiaihay.com