Đề kiểm tra 15 phút - Đề số 11 - Bài 4, 5 - Chương 1 - Hình học 8

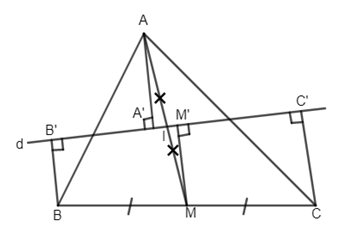
Đề bài

Cho tam giác ABC, trung tuyến AM. Vẽ đường thẳng d qua trung điểm I của AM, cắt các cạnh AB, AC. Gọi \(A',B',C'\) theo thứ tự là hình chiếu của A, B, C lên d. Chứng minh: \(BB' + CC' = 2AA'.\)

Lời giải chi tiết

Ta có \(BB' \bot d,CC' \bot d \Rightarrow BB'//CC'\) nên \(BB'C'C\) là hình thang.

M là trung điểm của BC (gt), \(MM' \bot d \Rightarrow MM'// BB'// CC'\) nên \(MM'\) là đường trung bình của hình thang \(BB'C'C\) ta có:

\(MM' = \dfrac{BB' + CC'} { 2}\) 

\(\Rightarrow BB' + CC' = 2MM'.\)

Xét \(\Delta AA'I\) và  \(\Delta MM'I\) có: 

IA=IM (gt)

\(\widehat {A'} = \widehat {M'} = {90^0}\)

\(\widehat {AIA'} = \widehat {MIM'}\) (đối đỉnh)

Suy ra \(\Delta AA'I = \Delta MM'I\) (cạnh huyền – góc nhọn) \( \Rightarrow AA' = MM'.\)

Vậy \(BB' + CC' = 2AA'.\)

Loigiaihay.com