Câu hỏi 5 trang 89 SGK Hình học 11

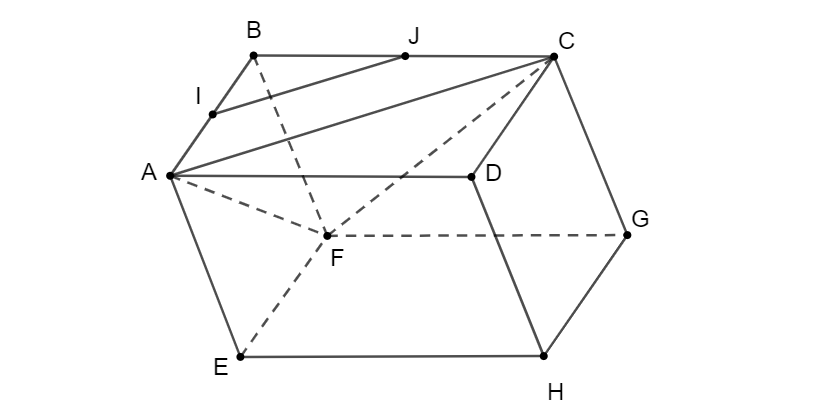
Đề bài

Cho hình hộp \(ABCD.EFGH\). Gọi \(I\) và \(K \) lần lượt là trung điểm của các cạnh \(AB\) và \(BC\). Chứng minh rằng các đường thẳng \(IK\) và \(ED\) song song với mặt phẳng \((AFC)\). Từ đó suy ra ba vecto \(\overrightarrow {{\rm{AF}}} ;\,\overrightarrow {IK} ;\,\overrightarrow {ED} \) đồng phẳng.

Lời giải chi tiết

\(I\) và \(K\) lần lượt là trung điểm của các cạnh \(AB\) và \(BC\) \(⇒ IK\) là đường trung bình của \(∆ABC\) nên \(IK//AC \subset \left( {ACF} \right) \Rightarrow IK//\left( {ACF} \right)\)

Hình hộp \(ABCD.EFGH\) nên \((ADHE) // (BCGF)\)

\(⇒ FC // ED\) (là đường chéo trong các hình bình hành \(BCGF\) và \(ADHE)\)

Nên \(ED // (AFC)\).

Ngoài ra \(AF \subset \left( {ACF} \right)\)

⇒ ba vecto \(\overrightarrow {{\rm{AF}}} ;\overrightarrow {IK} ;\overrightarrow {ED} \) đồng phẳng (vì giá của chúng song song với một mặt phẳng, có thể chọn một mặt phẳng bất kì song song với \((ACF)\))

 Loigiaihay.com