Câu hỏi:
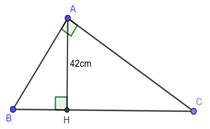
Cho tam giác \(ABC\) vuông tại \(A\) . Biết \(\frac{{AB}}{{AC}} = \frac{3}{7}\), đường cao \(AH = 42cm\). Tính \(BH,HC\).
- A \(BH = 18cm\,\,;\,\,\,HC = 98cm\)
- B \(BH = 24cm\,\,;\,\,\,HC = 72cm\)
- C \(BH = 20cm\,\,;\,\,\,HC = 78cm\)
- D \(BH = 28cm\,\,;\,\,\,HC = 82cm\)
Phương pháp giải:
Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(AC:\,\,\,\,\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}.\)
Kết hợp với giả thiết \(\frac{{AB}}{{AC}} = \frac{5}{6}\) để tính các cạnh \(AB,\,\,AC.\)
Áp dụng công thức hệ thức lượng trong tam giác vuông để tính cạnh \(HB:\,\,\,A{B^2} = HB.BC \Rightarrow HC.\)
Lời giải chi tiết:
Ta có: \(\frac{{AB}}{{AC}} = \frac{3}{7} \Rightarrow AB = \frac{3}{7}AC\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow \frac{1}{{{{42}^2}}} = \frac{{49}}{{9A{C^2}}} + \frac{1}{{A{C^2}}}\\ \Leftrightarrow \frac{1}{{{{42}^2}}} = \frac{{58}}{{9A{C^2}}} \Leftrightarrow A{C^2} = 11368\\ \Leftrightarrow AC = 14\sqrt {58} \,\,\left( {cm} \right)\\ \Rightarrow AB = \frac{3}{7}.14\sqrt {58} = 6\sqrt {58} \left( {cm} \right)\end{array}\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {\left( {6\sqrt {58} } \right)^2} + {\left( {14\sqrt {58} } \right)^2}\\ \Leftrightarrow B{C^2} = 13456 \Rightarrow BC = 116\,\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\( \Rightarrow A{B^2} = BH.BC\)\( \Leftrightarrow {\left( {6\sqrt {58} } \right)^2} = 116.BH \Leftrightarrow BH = 18\left( {cm} \right)\)
\( \Rightarrow CH = BC - BH = 116 - 18 = 98\,\,\,\left( {cm} \right).\)
Chọn A.