Câu hỏi:
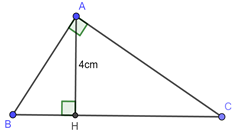
Cho tam giác \(ABC\) vuông tại \(A,\) kẻ đường cao \(AH.\) Biết \(AH = 4cm,\,\,\,\frac{{HB}}{{HC}} = \frac{1}{4}.\) Tính chu vi tam giác\(ABC.\)
- A \(5\sqrt{5} + 8\,\,cm\)
- B \(6\sqrt{5} + 12\,\,cm\)
- C \(4\sqrt{5} + 8\,\,cm\)
- D \(6\sqrt{5} + 10\,\,cm\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông và giả thiết bài toán để tính các cạnh HB, HC từ đó suy ra độ dài cạnh BC.
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH để tính độ dài cạnh AB, AC.
Khi đó chu vi tam giác ABC là: \(AB + AC + BC.\)
Lời giải chi tiết:
Ta có: \(\frac{{HB}}{{HC}} = \frac{1}{4} \Rightarrow HC = 4HB\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\( \Rightarrow A{H^2} = BH.CH\)\( \Leftrightarrow {4^2} = 4B{H^2} \Leftrightarrow BH = 2\,\,\,\left( {cm} \right)\)\( \Rightarrow CH = 8\left( {cm} \right)\)
Ta có: \(BC = BH + HC = 2 + 8 = 10\,\,\,\left( {cm} \right)\,\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\( \Rightarrow A{B^2} = BH.BC\)\( \Leftrightarrow A{B^2} = 2.10\)\( \Leftrightarrow AB = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow 20 + A{C^2} = 100 \Leftrightarrow A{C^2} = 80\)\( \Rightarrow AC = \sqrt {80} = 4\sqrt 5 \,\,cm.\)
Vậy chu vi tam giác\(ABC\) là: \(4\sqrt 5 + 2\sqrt 5 + 10 = 6\sqrt 5 + 10\,\,cm.\)
Chọn D.