Phương pháp giải:

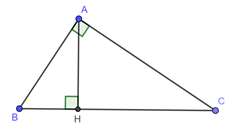
Giả sử tam giác đã cho là $\Delta ABC$ vuông tại $A$  có $AB < AC,\,\,\,BC = 5,\,\,\,AH = 2.$

Đặt $BH = x\,\,\,\left( {0 < x < 2,5} \right).$

Khi đó áp dụng hệ thức lượng trong tam giác vuông và định lý Pitago để tính $x$ và từ đó suy ra độ dài các cạnh của tam giác.

Lời giải chi tiết:

Giả sử tam giác đã cho là $\Delta ABC$ vuông tại $A$  có $AB < AC,\,\,\,BC = 5,\,\,\,AH = 2.$

Đặt $BH = x\,\,\,\left( {0 < x < 2,5} \right) \Rightarrow HC = 5 - x.$

Áp dụng hệ thức lượng trong $\Delta ABC$ vuông tại $A$ có đường cao $AH$ ta có:

$\Rightarrow A{H^2} = BH.CH \Leftrightarrow {2^2} = x\left( {5 - x} \right)$

$\Leftrightarrow {x^2} - 5x + 4 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\left( {tm} \right)\\x = 4\,\,\,\left( {ktm} \right)\end{array} \right.$

$\Rightarrow A{B^2} = BC.BH = 5.1 = 5 \Leftrightarrow AB = \sqrt 5 .$

Vậy cạnh nhỏ nhất của tam giác đã cho có độ dài là $\sqrt 5 .$

Chọn A.