Câu hỏi 1 trang 100 SGK Đại số 10

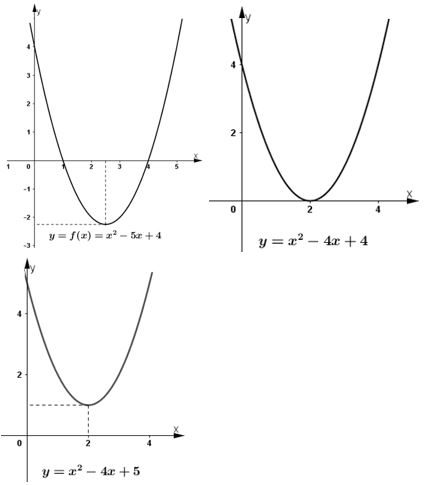
LG 1

Xét tam thức bậc hai f(x) = x² – 5x + 4. Tính f(4), f(2), f(-1), f(0) và nhận xét về dấu của chúng.

Phương pháp giải:

Thay lần lượt  x= 4, x=2, x=-1, x=0 vào f(0) để suy ra f(4), f(2), f(-1), f(0) tương ứng.

So sánh kq thu được với 0.

Lời giải chi tiết:

f(x) = x² – 5x +4

\(\begin{array}{l}
f\left( 4 \right) = {4^2} - 5.4 + 4 = 0\\
f\left( 2 \right) = {2^2} - 5.2 + 4 = - 2 < 0\\
f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 5.\left( { - 1} \right) + 4 = 10 > 0\\
f\left( 0 \right) = {0^2} - 5.0 + 4 = 4 > 0
\end{array}\)

LG 2

Quan sát đồ thị hàm số y = x² – 5x + 4 (h.32a)) và chỉ ra các khoảng trên đó đồ thị ở phía trên, phía dưới trục hoành.

Lời giải chi tiết:

Với 1 < x < 4 thì đồ thị nằm phía dưới trục hoành.

Với x < 1 hoặc x > 4 thì đồ thị nằm phía trên trục hoành.

LG 3

Quan sát các đồ thị trong hình 32 và rút ra mối liên hệ về dấu của giá trị f(x) = ax² + bx + c ứng với x tùy theo dấu của biệt thức Δ = b² – 4ac

Lời giải chi tiết:

Hình 32a) có Δ > 0 ⇒ f(x) cùng dấu với a khi x nằm ngoài khoảng hai nghiệm của phương trình f(x) = 0; f(x) trái dấu với a khi x nằm trong khoảng hai nghiệm của phương trình f(x) = 0.

Hình 32b) có Δ = 0 ⇒ f(x) cùng dấu với a, trừ khi x = - b/2a.

Hình 32c) có Δ < 0 ⇒ f(x) cùng dấu với a.

Loigiaihay.com