Bài 3 trang 105 SGK Đại số 10Giải các bất phương trình sau... Quảng cáo
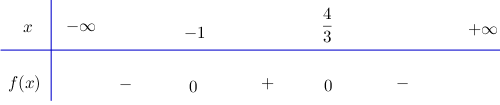
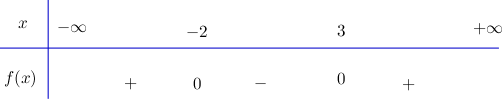
Video hướng dẫn giải Giải các bất phương trình sau LG a \(4{x^2} - x + 1 < 0\); Phương pháp giải: Sử dụng cách xét dấu của nhị thức bậc nhất và tam thức bậc hai để giải bất phương trình. Lời giải chi tiết: Tam thức \(f(x) =4{x^2} - x + 1 < 0\) có hệ số \(a = 4 > 0\) biệt thức \(∆ = (-1)^2- 4.4.1=-15 < 0\). Do đó \(f(x) > 0 ,∀x ∈\mathbb R\). Vậy bất phương trình \(4{x^2} - x + 1 < 0\) vô nghiệm. Cách khác: \(4{x^2} - x + 1 \) \(= {\left( {2x} \right)^2} - 2.2x.\dfrac{1}{4} + \dfrac{1}{{16}} + \dfrac{{15}}{{16}} \) \( = {\left( {2x - \dfrac{1}{4}} \right)^2} + \dfrac{{15}}{{16}} \ge \dfrac{{15}}{{16}} > 0, \forall x\in R\) Do đó bpt \(4{x^2} - x + 1 < 0\) vô nghiệm. LG b \( - 3{x^2} + x + 4 \ge 0\); Lời giải chi tiết: \( - 3{x^2} + x + 4 \ge 0\) Ta xét: \(f(x) = - 3{x^2} + x + 4 = 0 \) \(\Leftrightarrow \left[ \matrix{ Ta có bảng xét dấu: Do đó: \( - 3{x^2} + x + 4 \ge 0 \Leftrightarrow - 1 \le x \le {4 \over 3}.\) LG c \(\dfrac{1}{x^{2}-4}<\dfrac{3}{3x^{2}+x-4};\) Lời giải chi tiết: \(\dfrac{1}{x^{2}-4}<\dfrac{3}{3x^{2}+x-4}\) \( \Leftrightarrow \dfrac{1}{x^{2}-4}-\dfrac{3}{3x^{2}+x-4}< 0\) \( \Leftrightarrow \dfrac{{3{x^2} + x - 4 - 3{x^2} + 12}}{{\left( {{x^2} - 4} \right)\left( {3{x^2} + x - 4} \right)}} < 0\) \( \Leftrightarrow \dfrac{x+8}{(x^{2}-4)(3x^{2}+x-4)}< 0\) Lập bảng xét dấu vế trái: + Nhị thức \(x + 8\) có nghiệm \(x = -8\) + Tam thức \( x^{2} – 4\) có hai nghiệm \(x = 2\) và \(x = -2\), hệ số \(a = 1 > 0\) Do đó \( x^{2} – 4\) mang dấu + khi\( x < -2\) hoặc \(x > 2\) và mang dấu – khi \(-2 < x < 2\). + Tam thức \( 3x^{2}+x – 4\) có hai nghiệm \(x = 1\) và \(x = -4/3\), hệ số \( a = 3 > 0\) Do đó \( 3x^{2}+x – 4\) mang dấu + khi \(x < -4/3 \) hoặc \(x > 1\), mang dấu – khi \(-4/3 < x < 1\). Bảng xét dấu: Tập nghiệm của bất phương trình \(S = (-∞; - 8) ∪ \left(- 2; -\dfrac{4}{3}\right) ∪ (1; 2)\). LG d \(x^2- x - 6 ≤ 0\). Lời giải chi tiết: \(x^2- x - 6 ≤ 0\) \(x^2- x - 6 =0\) \( \Leftrightarrow \left[ \matrix{ Ta có bảng xét dấu: Tập nghiệm của bất phương trình là: \(S =[- 2; 3]\). Loigiaihay.com
|





















Danh sách bình luận