Bài 8 trang 50 SGK Đại số 10Tìm tập xác định của các hàm số Quảng cáo
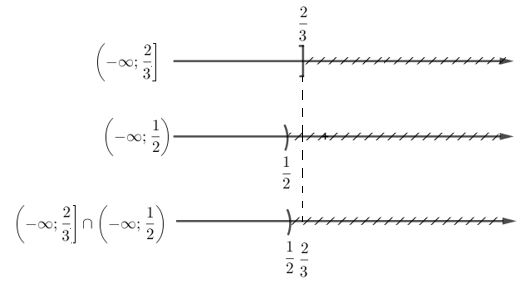
Video hướng dẫn giải Tìm tập xác định của các hàm số LG a \(y = {2 \over {x + 1}} + \sqrt {x + 3}\) Phương pháp giải: +) Hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định khi \(g(x) \neq 0.\) +) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\) Lời giải chi tiết: \(y = {2 \over {x + 1}} + \sqrt {x + 3}\) Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l} Tập xác định: \(D = \left[ { - 3; + \infty } \right)\backslash \left\{ -1 \right\} \)\(= \left[ { - 3; - 1} \right) \cup \left( {-1; + \infty } \right).\) LG b \(y = \sqrt {2 - 3x} - {1 \over {\sqrt {1 - 2x} }}\) Phương pháp giải: +) Hàm số \(y = \frac{{f\left( x \right)}}{{\sqrt {g\left( x \right)} }}\) xác định khi \(g(x) > 0.\) +) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\) Lời giải chi tiết: \(y = \sqrt {2 - 3x} - {1 \over {\sqrt {1 - 2x} }}\) Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l} Tập xác định: \(D = \left( { - \infty ;\frac{1}{2}} \right).\) Chú ý: Các em dùng trục số để lấy giao hai tập hợp như sau: LG c \(y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.\) Phương pháp giải: +) Hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định khi \(g(x) \neq 0.\) +) Hàm số: \(y = \sqrt {f\left( x \right)} \) xác định khi \(f(x) \geq 0.\) Lời giải chi tiết: + Xét trên \(\left[ {1; + \infty } \right)\) thì \(y = \frac{1}{{x + 3}}\) Hàm số xác định khi x + 3 ≠ 0 (luôn thỏa mãn với mọi x ≥ 1). Vậy hàm số luôn xác định trên [1; +∞). + Xét trên (–∞; 1) thì \(y = \sqrt {2 - x} \) Hàm số xác định khi 2 – x ≥ 0 ⇔ x ≤ 2 (luôn thỏa mãn với mọi x < 1). Vậy hàm số luôn xác định trên (–∞; 1). Kết luận: Hàm số xác định trên R. Cách trình bày khác: \(y = \left\{ \matrix{{1 \over {x + 3}} \, \, khi \, \, x \ge 1 \hfill \cr \sqrt {2 - x} \, \, \, khi \, \, x < 1 \hfill \cr} \right.\) Hàm số xác định \( \Leftrightarrow \left[ \begin{array}{l} \(\Leftrightarrow x\in R\). Tập xác định: \(D = R.\) Loigiaihay.com
|




















Danh sách bình luận