Bài 6 trang 27 (Ôn tập chương I - Vectơ) SGK Hình học 10

LG a

 $|\overrightarrow {AB}  + \overrightarrow {AC} |$

Phương pháp giải:

Kẻ đường cao AH suy ra H là trung điểm BC.

Tính $\overrightarrow {AB} + \overrightarrow {AC}$ theo $\overrightarrow {AH}$ dựa vào tính chất trung điểm.

Tính AH dựa vào tỉ số lượng giác của góc nhọn trong tam giác vuông.

(Chú ý: cạnh góc vuông bằng cạnh huyền nhân sin góc đối)

Lời giải chi tiết:

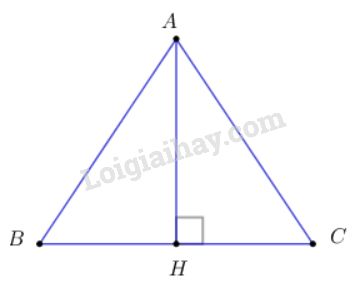
Hạ $AH\bot BC$ do tam giác $ABC$ đều nên $H$ là trung điểm của $BC$.

Ta có:

$\eqalign{ & \overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AH} \cr  & \Rightarrow |\overrightarrow {AB} + \overrightarrow {AC} | = 2|\overrightarrow {AH} | = 2AH \cr}$

Xét tam giác ABH vuông tại H có:

AB=a, $\widehat {ABH} = {60^0}$ nên $AH = AB\sin {60^0} = a.\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}$

$\Rightarrow |\overrightarrow {AB}  + \overrightarrow {AC} | =2AH$ $=2.\frac{{a\sqrt 3 }}{2}= a\sqrt 3$

Cách khác:

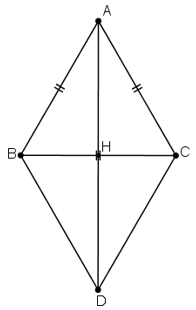
Vẽ hình bình hành ABDC, gọi H là giao điểm của AD và BC.

Ta có:

$\begin{array}{l}\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \\ \Rightarrow \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\end{array}$

+ Hình bình hành ABDC có AB = AC ⇒ ABDC là hình thoi ⇒ AD ⊥ BC tại H.

+ H là trung điểm BC ⇒ BH = BC/2 = a/2.

+ ΔABH vuông tại H nên:

$AH = \sqrt {A{B^2} - B{H^2}}$ $= \sqrt {{a^2} - \frac{{{a^2}}}{4}}  = \frac{{a\sqrt 3 }}{2}$

+ H là trung điểm AD ⇒ AD = 2. AH = a√3.

Vậy $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = a\sqrt 3$.

LG b

$|\overrightarrow {AB}  - \overrightarrow {AC} |$

Lời giải chi tiết:

Ta có: $\overrightarrow {AB}  - \overrightarrow {AC} =\overrightarrow {CB}$

Suy ra $|\overrightarrow {AB}  - \overrightarrow {AC} | = |\overrightarrow {CB} | = CB = a$

Loigiaihay.com