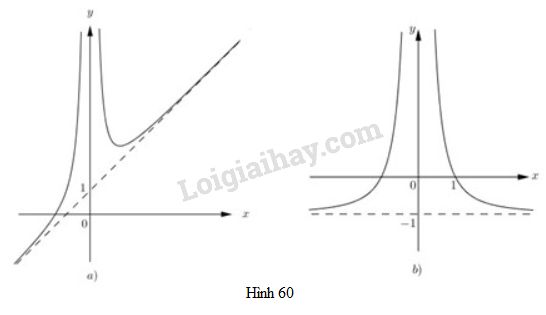
Bài 6 trang 142 SGK Đại số và Giải tích 11

LG a

Tính \(\mathop {\lim }\limits_{x \to 0} f(x);\mathop {\lim }\limits_{x \to 0} g(x);\mathop {\lim }\limits_{x \to  + \infty } f(x);\mathop {\lim }\limits_{x \to  + \infty } g(x)\)

Phương pháp giải:

+) Tính giới hạn khi \(x\) tiến đến 0: Đánh giá giới hạn \(\frac{L}{0}\)

+) Tính giới hạn khi \(x\) tiến ra vô cùng: Chia cả tử và mẫu cho \(x\) mũ bậc cao nhất của cả tử và mẫu.

Lời giải chi tiết:

+)  \(\mathop {\lim }\limits_{x \to 0} f(x) = \mathop {\lim }\limits_{x \to 0} {{1 - {x^2}} \over {{x^2}}} =  + \infty \)

Vì: \(\mathop {\lim }\limits_{x \to 0} (1 - {x^2}) = 1 > 0,\)

     \(\mathop {\lim }\limits_{x \to 0} {x^2} = 0;{x^2} > 0,\forall x \ne 0\)

+)  \(\mathop {\lim }\limits_{x \to 0} g(x) = \mathop {\lim }\limits_{x \to 0} {{{x^3} + {x^2} + 1} \over {{x^2}}} =  + \infty \)

Vì: \(\mathop {\lim }\limits_{x \to 0} ({x^3} + {x^2} + 1) = 1 > 0,\mathop {\lim }\limits_{x \to 0} {x^2} = 0,{x^2} > 0,\) \(\forall x \ne 0\)

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } {{1 - {x^2}} \over {{x^2}}} \cr 
& = \mathop {\lim }\limits_{x \to + \infty } {{{x^2}({1 \over {{x^2}}} - 1)} \over {{x^2}}} = \mathop {\lim }\limits_{x \to + \infty } ({1 \over {{x^2}}} - 1) = - 1 \cr} \) 

\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } {{{x^3} + {x^2} + 1} \over {{x^2}}} \cr&= \mathop {\lim }\limits_{x \to + \infty } {{{x^3}(1 + {1 \over x} + {1 \over {{x^3}}})} \over {{x^3}({1 \over x})}} \cr 
& = \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x} + {1 \over {{x^3}}}} \over {{1 \over x}}} = + \infty \cr} \)

Câu 2

Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường cong nào là đồ thị của mỗi hàm số đó.

Phương pháp giải:

+) Tính giới hạn khi \(x\) tiến đến 0: Đánh giá giới hạn \(\frac{L}{0}\)

+) Tính giới hạn khi \(x\) tiến ra vô cùng: Chia cả tử và mẫu cho \(x\) mũ bậc cao nhất của cả tử và mẫu.

Lời giải chi tiết:

Gọi \((C_1)\) và \((C_2)\) lần lượt là hai đồ thị của hàm số \(y = f(x)\) và \(y = g(x)\)

+)  Vì \(\mathop {\lim }\limits_{x \to  + \infty } f(x) =  - 1\) nên \((C_1)\) có nhánh vô tận tiến gần đến đường thẳng \(y = -1\) \(khi x \rightarrow  ∞\)

+)  Vì \(\mathop {\lim }\limits_{x \to  + \infty } g(x) =  + \infty \) \((C_2)\) có nhánh vô tận đi lên khi \(x \rightarrow +∞\)

Dựa vào đặc điểm của \((C_1)\) và \((C_2)\)  như trên ta có\((C_1)\)  là đồ thị b và \((C_2)\)  là đồ thị a.

 Loigiaihay.com