Bài 5 trang 6 SBT Hình Học 11 nâng caoGiải bài 5 trang 6 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác DNM nằm trên (O; R). Quảng cáo
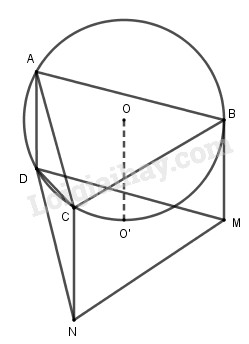
Đề bài Cho tứ giác ABCD nội tiếp đường tròn (O; R) trong đó AD = R. Dựng các hình bình hành DABM và DACN. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác DNM nằm trên (O; R). Lời giải chi tiết Theo giả thiết ta có: \(\overrightarrow {AD} = \overrightarrow {BM} = \overrightarrow {CN} \) Vì vậy, phép tịnh tiến theo vecto \(\overrightarrow {AD} \) biến tam giác ABC thành tam giác DMN. Suy ra, nếu O’ là tâm đường tròn ngoại tiếp tam giác DMN thì phép tịnh tiến đó biến O thành O’, tức là: \(\overrightarrow {OO'} = \overrightarrow {AD} \) Do đó: OO' = AD = R Và vì vậy O’ nằm trên (O; R).
Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
