Câu 4.25 trang 105 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.25 trang 105 SBT Đại số 10 Nâng cao. Quảng cáo
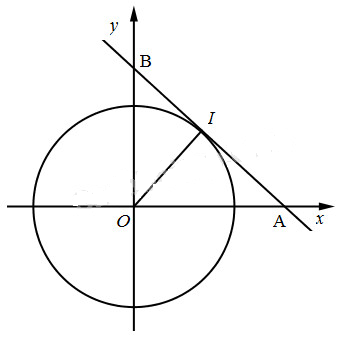
Đề bài Trên mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O có bán kính R (R > 0). Trên các tia Ox và Oy lần lượt lấy hai điểm A và B sao cho đường thẳng AB luôn tiếp xúc với đường tròn đó. Hãy xác định tọa độ của A và B để tam giác OAB có diện tích nhỏ nhất. Lời giải chi tiết
Ta có \(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}OI.AB = \dfrac{{\rm{R}}}{2}.AB;\\AB = IA + IB \ge 2\sqrt {IA.IB} = 2\sqrt {{\rm{O}}{I^2}} = 2{\rm{R}};\\AB = 2{\rm{R}} \Leftrightarrow IA = IB = R.\end{array}\) Lúc đó tam giác OAB vuông cân tại O, Cạnh huyền \(AB = 2R.\) \(OA = OB = R\sqrt 2 \) Suy ra \({S_{OAB}} \ge \dfrac{{\rm{R}}}{2}.2{\rm{R}} = {R^2}.\) Vậy \({S_{OAB}}\) nhỏ nhất bằng \({R^2}\) khi \(OA = OB = R\sqrt 2 .\) Khi đó tọa độ \(A\left( {{\rm{R}}\sqrt 2 ;0} \right)\) và \(B\left( {0;R\sqrt 2 } \right).\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
