Bài 3 trang 6 SBT Hình Học 11 nâng caoGiải bài 3 trang 6 sách bài tập Hình Học 11 nâng cao. Tìm quỹ tích trực tâm các tam giác MPQ và NPQ. Quảng cáo
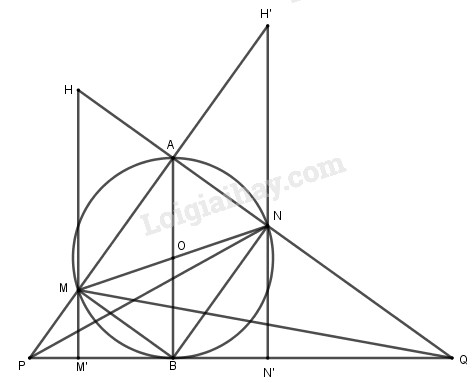
Đề bài Cho đường tròn (O) với đường kính AB cố định một đường kính MN thay đổi. Các đường thẳng AM và AN cắt tiếp tuyến tại B lần lượt tại P và Q. Tìm quỹ tích trực tâm các tam giác MPQ và NPQ. Lời giải chi tiết
Tam giác MPQ có QA là một đường cao ( vì \(QA \bot MP\)). Kẻ \(MM' \bot PQ\) thì MM’ cắt QA tại trực tâm H của tam giác MPQ OA là đường trung bình của tam giác NMH nên: \(\overrightarrow {MH} = 2\overrightarrow {OA} = \overrightarrow {BA} \) Vậy phép tịnh tiến T theo vecto \(\overrightarrow {BA} \) biến M thành H. Chú ý rằng M không trùng với A hoặc B, ta suy ra quỹ H là ảnh của đường tròn (O) (không kể hai điểm A và B) qua phép tịnh tiến đó. Làm tương tự đối với trực tâm H’ của tam giác NPQ. Quỹ tích điểm H' là ảnh của đường tròn (O) (không kể hai điểm A và B) qua phép tịnh tiến T theo vecto \(\overrightarrow {BA} \). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
