Bài 2.36 trang 36 SBT Đại số 10 Nâng cao

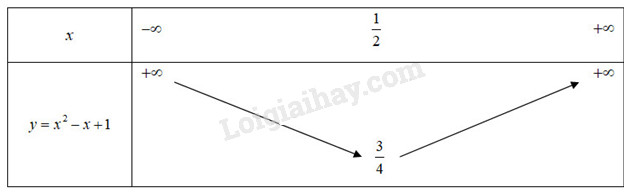
LG a

Xác định các hệ số \(a, b\) và \(c\). Khảo sát sự biến thiên và vẽ đồ thị \((P)\) của hàm số nhận được.

Lời giải chi tiết:

● Vì hàm số có giá trị nhỏ nhất bằng \({3 \over 4}\) khi \(x = {1 \over 2}\) nên \( - {b \over {2a}} = {1 \over 2}\) và \( - {\Delta  \over {4a}} =  - {{{b^2} - 4ac} \over {4a}} = {3 \over 4},\) suy ra \(a = -b\) và \(–a + 4c = 3.\)

Vì hàm số có giá trị bằng 1 khi \(x = 1\) nên \(f(1) = a + b + c = 1\), suy ra \(c = 1\) (do \(a = -b\)). Do đó \(a = 4c – 3 = 1\) và \(b = -1\).

Vậy hàm số cần tìm là \(y = {x^2} - x + 1\)

●Do hệ số \(a = 1 > 0\) và giá trị nhỏ nhất của hàm số đạt được tại \(x = {1 \over 2}\) nên hàm số nghịch biến trên khoảng \(\left( { - \infty ;{1 \over 2}} \right)\) và đồng biến trên khoảng \(\left( {{1 \over 2}; + \infty } \right).\)

Bảng biến thiên :

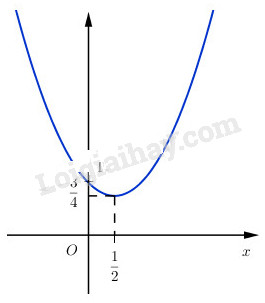
Hàm số có đồ thị

LG b

Xét đường thẳng \(y = mx\), kí hiệu bởi \((d)\). Khi \((d)\) cắt \((P)\) tại hai điểm \(A\) và \(B\) phân biệt, hãy xác định tọa độ trung điểm của đoạn thẳng \(AB.\)

Lời giải chi tiết:

Đường thẳng \(y = mx\) cắt parabol \((P)\)

tại hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) nếu

và chỉ nếu phương trình \({x^2} - x + 1 = mx\) hay

\({x^2} - \left( {1 + m} \right)x + 1 = 0\)           (1)

Có hai nghiệm phân biệt, tức là biệt thức \(\Delta  = {\left( {1 + m} \right)^2} - 4 = {m^2} + 2m - 3\) dương.

Khi đó, hai nghiệm của (1) chính là \(x_A\) và \(x_B\). Theo định lí Vi-ét, ta có

\({x_A} + {x_B} = 1 + m\)                  (2)

Từ (2) ta suy ra hoành độ trung điểm \(C\) của đoạn thẳng \(AB\) là

\({x_C} = {{{x_A} + {x_B}} \over 2} = {{1 + m} \over 2}.\)

Do \(C\) là một điểm thuộc đường thẳng \((d)\) nên tung độ \(y_C\) của nó thỏa mãn

\({y_C} = m{x_C} = {{m\left( {1 + m} \right)} \over 2}\)

Kết luận. Tọa độ trung điểm của đoạn thẳng \(AB\) là \(C\left( {{{1 + m} \over 2};{{m\left( {1 + m} \right)} \over 2}} \right)\) với điều kiện \({m^2} + 2m - 3 > 0.\)

Loigiaihay.com