Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng caoChứng minh rằng phương trình Quảng cáo
Đề bài Chứng minh rằng phương trình \({x^3} + a{x^2} + bx + c = 0\) luôn có ít nhất một nghiệm. Lời giải chi tiết Đặt \(f(x)={x^3} + a{x^2} + bx + c = 0\)
Do \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \) nên có số \(α < 0\) sao cho \(f(α) < 0\). Do \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên có số \(β > 0\) sao cho \(f(β) > 0\). Hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) liên tục trên \(\mathbb R\) chứa đoạn \(\left[ {\alpha ;\beta } \right]\) nên theo định lý về giá trị trung gian của hàm số liên tục, tồn tại số \(d \in \left[ {\alpha ;\beta } \right]\) sao cho \(f(d) = 0\). Đó chính là nghiệm của phương trình \(f(x) = 0\). Loigiaihay.com
|














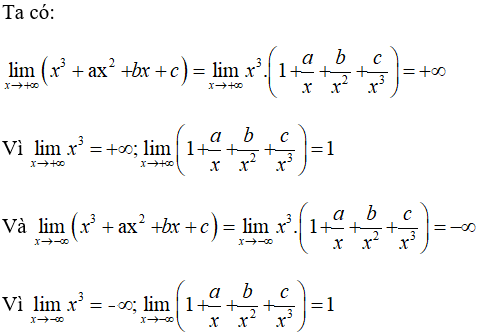






Danh sách bình luận