Câu 2 trang 91 SGK Hình học 11 Nâng caoCho hình chóp S.ABCD. Quảng cáo
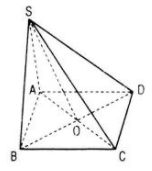
Đề bài Cho hình chóp S.ABCD. a. Chứng minh rằng nếu ABCD là hình bình hành thì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \). Điều ngược lại có đúng không ? b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) Lời giải chi tiết
a. Ta có: \(\eqalign{ & \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \cr & \Leftrightarrow \overrightarrow {SB} - \overrightarrow {SC} = \overrightarrow {SA} - \overrightarrow {SD} \cr&\Leftrightarrow \overrightarrow {CB} = \overrightarrow {DA} \cr} \) ⇔ ABCD là hình bình hành. b. Ta có: \(\eqalign{ & \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} \cr& + \overrightarrow {SO} + \overrightarrow {OC} + \overrightarrow {SO} + \overrightarrow {OD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \,\,\left( * \right) \cr} \) Nếu ABCD là hình bình hành thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) suy ra \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) (do (*)) Ngược lại, giả sử \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} ,\) ta có (*). Gọi M, N lần lượt là trung điểm của AC, BD thì : \(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {OM} ,\overrightarrow {OB} + \overrightarrow {OD} = 2\overrightarrow {ON} \) Từ (*) suy ra \(2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 ,\) điều này chứng tỏ O, M, N thẳng hàng Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành. Loigiaihay.com
|




















Danh sách bình luận