Bài 10 trang 120 SGK Hình học 11

Đề bài

Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác \(ABC\) là đường vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).

Lời giải chi tiết

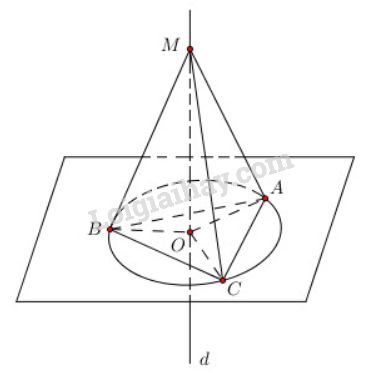
Lấy một điểm \(M\) bất kì trong không gian sao cho \(MA  = MB = MC\). Từ \(M\) kẻ \(MO\) vuông góc với \((ABC)\). Các tam giác vuông \(MOA\), \(MOB\), \(MOC\) bằng nhau, suy ra \(OA = OB = OC\).

Do đó \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Vậy các điểm \(M\) cách đều ba đỉnh của tam giác \(ABC\) nằm trên đường thẳng \(d\) đi qua tâm \(O\) của đường tròn ngoại tiếp tam giác \(ABC\) và vuông góc với mặt phẳng \((ABC)\).

Ngược lại, lấy một điểm \(M’ ∈ d\), nối \(M’A, M’B, M’C\),

Do \(M’O\) chung và \(OA = OB = OC\) nên các tam giác vuông \(M’OA, M’OB, M’OC\)  bằng nhau, suy ra \(M’A = M’B = M’C\),

Tức là điểm \(M’\) cách đều ba đỉnh \(A, B, C\) của tam giác \(ABC\).

Kết luận: Tập hợp các điểm cách đều ba đỉnh của tam giác \(ABC\) là đường thẳng vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).

 Loigiaihay.com