Các dạng toán về đường thẳng vuông góc với mặt phẳng

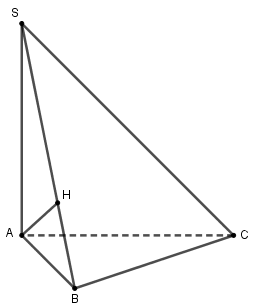
Dạng 1: Chứng minh đường thẳng vuông góc với mặt phẳng

Phương pháp:

Muốn chứng minh đường thẳng $d \bot \left( \alpha  \right)$ ta có thể dùng một trong hai cách sau.

Cách 1. Chứng minh $d$ vuông góc với hai đường thẳng $a,b$ cắt nhau trong $\left( \alpha  \right)$.

Kí hiệu: $\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \subset \left( \alpha  \right),b \subset \left( \alpha  \right)\\a \cap b = I\end{array} \right. \Rightarrow a \bot \left( \alpha  \right)$

Cách 2. Chứng minh $d$ song song với đường thẳng $a$ mà $a$ vuông góc với $\left( \alpha  \right)$.

Kí hiệu: $\left\{ \begin{array}{l}d\parallel a\\\left( \alpha  \right) \bot a\end{array} \right. \Rightarrow d \bot \left( \alpha  \right)$

Cách 3. Chứng minh $d$ vuông góc với $\left( Q \right)$ và $\left( Q \right)//\left( P \right)$.

Dạng 2: Chứng minh hai đường thẳng vuông góc bằng cách dùng đường thẳng vuông góc mặt phẳng

Phương pháp:

Để chứng minh $d \bot \;a$, ta có thể chứng minh bởi một trong các cách sau:

Cách 1: Chứng minh $d$ vuông góc với $\left( P \right)$ và $\left( P \right)$ chứa $a$.

Cách 2: Sử dụng định lí ba đường vuông góc.

Cách 3: Sử dụng các cách chứng minh đã biết ở phần trước.

Ví dụ:

Cho tứ diện \(SABC\) có tam giác \(ABC\) vuông tại \(B\), \(SA \bot \left( {ABC} \right)\)

a) Chứng minh: \(BC \bot \left( {SAB} \right)\)

b) Gọi \(AH\) là đường cao của \(\Delta SAB\). Chứng minh: \(AH \bot SC\)

Giải

a) Ta có: \(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\BC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow SA \bot BC\)

Mà \(BC \bot AB\) (do tam giác \(ABC\) vuông tại \(B\))

Nên \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) (đpcm)

b) Do \(\left\{ \begin{array}{l}BC \bot \left( {SAB} \right)\\AH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow BC \bot AH\) (1)

Lại có \(AH \bot SB\) (2)

Từ (1) và (2) suy ra \(AH \bot \left( {SBC} \right)\)

Mà \(SC \subset \left( {SBC} \right) \Rightarrow AH \bot SC\) (đpcm).