Bài tập 6 trang 152 Tài liệu dạy – học Toán 7 tập 1Giải bài tập Cho tam giác ABC có Quảng cáo
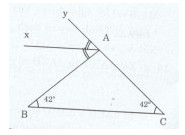
Đề bài Cho tam giác ABC có \(\widehat B = \widehat C = {42^o}\) . Gọi Ax là tia phân giác của góc ngoài tại đỉnh A. Chứng tỏ rằng Ax // BC. Lời giải chi tiết Vẽ tia Ay là tia đối của tia AC tại A Ta có: \(\widehat {yAB} = \widehat {ABC} + \widehat {ACB}\) (góc ngoài của tam giác ABC) \( \Rightarrow \widehat {yAB} = {42^0} + {42^0} = {84^0}\) Mà Ax là tia phân giác của góc yAB Nên \(\widehat {yAx} = \widehat {xAB} = {{\widehat {yAB}} \over 2} = {{{{84}^0}} \over 2} = {42^0}\) Ta có: \(\widehat {xAB} = \widehat {ABC}( = {42^0})\) Và hai góc xAB và ABC nằm ở vị trí so le trong nên Ax // BC. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
