Bài tập 4 trang 122 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Tam giác đều lớn có cạnh là 8 cm. Khi gấp tam giác theo đường có gạch chấm, em có thể tạo thành hình chóp được không ? Tính diện tích toàn phần hình chóp đó ? Quảng cáo
Đề bài Tam giác đều lớn có cạnh là 8 cm. Khi gấp tam giác theo đường có gạch chấm, em có thể tạo thành hình chóp được không ? Tính diện tích toàn phần hình chóp đó ? Lời giải chi tiết Khi gấp tam giác theo đường có gạch chấm ta nhận được hình chóp tam giác đều. M, N lần lượt là trung điểm của AB và AC (gt) =>MN là đường trung bình của tam giác ABC \( \Rightarrow MN = {{BC} \over 2} = {8 \over 2} = 4(cm)\) Đáy của hình chóp là tam giác đều cạnh 4cm Chiều cao của tam giác đáy là: \(HN = \sqrt {M{N^2} - M{H^2}} = \sqrt {{4^2} - {2^2}} \)\(\, = \sqrt {12} (cm)\) Diện tích đáy của hình chóp đều là: \({S_d} = {1 \over 2}HN.MP \)\(\,= {1 \over 2}\sqrt {12} .4 = 2\sqrt {12} (c{m^2})\) Trung đoạn của tam giác bên là: \(AH = \sqrt {A{P^2} - H{P^2}} \)\(\,= \sqrt {{4^2} - {2^2}} = \sqrt {12} (cm)\) Diện tích xung quanh của hình chóp đều: \({S_{xq}} = p.h\)\(\, = {1 \over 2}(MN + NP + MP).AH \)\(\,= {1 \over 2}.12.\sqrt {12} = 6\sqrt {12} (c{m^2})\) Diện tích toàn phần hình chóp đều: \({S_{tp}} = {S_{xq}} + {S_d} = 6\sqrt {12} + 2\sqrt {12} \)\(\, = 8\sqrt {12} (c{m^2})\) Loigiaihay.com
|














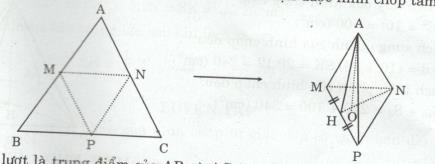






Danh sách bình luận