Bài tập 29 trang 92 Tài liệu dạy – học Toán 8 tập 2

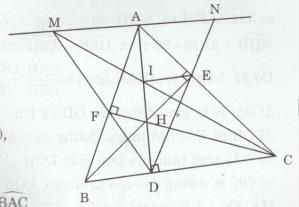
Đề bài

Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh rằng : \(\Delta BDA \sim \Delta BFC\) và BD.BC = BF.BA

b) Chứng minh rằng \(\widehat {BDF} = \widehat {BAC}\) .

c) CHứng minh rằng BH.BE = BD.BC và \(BH.BE{\rm{ }} + {\rm{ }}CH.CF{\rm{ }} = B{C^2}\) .

d) Đường thẳng qua A song song với BC cắt tia DF tại M. Gọi I là giao điểm của CM và AD. Chứng minh rằng IE // BC.

Lời giải chi tiết

a) Xét ∆BDA và ∆BFC có:

\(\widehat {DBA}\) (chung), \(\widehat {BDA} = \widehat {BFC}( = 90^\circ )\)

Do đó \(\Delta BDA \sim \Delta BFC(g.g)\)

\( \Rightarrow {{BD} \over {BF}} = {{BA} \over {BC}} \)

\(\Rightarrow BD.BC = BF.BA\)

b) Xét ∆BDF và ∆BAC có: \(\widehat {DBF}(chung),\)

\({{BD} \over {BA}} = {{BF} \over {BC}}\) (vì BD.BC = BF.BA)

Do đó \(\Delta BDF \sim \Delta BAC(c.g.c) \)

\(\Rightarrow \widehat {BDF} = \widehat {BAC}\)

c) Xét ∆BDH và ∆BEC có: \(\widehat {DBH}(chung),\widehat {BDH} = \widehat {BEC}( = 90^\circ )\)

Do đó \(\Delta BDH \sim \Delta BEC(g.g) \)

\(\Rightarrow {{BD} \over {BE}} = {{BH} \over {BC}} \)

\(\Rightarrow BH.BE = BD.BC\)

Tương tự có \(\Delta CDH \sim \Delta CFB \)

\(\Rightarrow {{CH} \over {BC}} = {{CD} \over {CF}}\)

\(\Rightarrow CH.CF = CD.BC\)

Do đó \(BH.BE + CH.CF \)\(\,= BD.BC + CD.BC\)\(\, = BC.(BD + CD) = BC.BC= {BC^2}\)

d) Gọi N là giao điểm của DE và AM, ta có \(\widehat {BDF} = \widehat {BAC}(\Delta BDF \sim \Delta BAC)\)

Tương tự \(\widehat {CDE} = \widehat {CAB}\)

Do đó \(\widehat {BDF} = \widehat {CDE}.\)

Mà \(\widehat {BDF} + \widehat {ADM} = \widehat {CDE} + \widehat {ADN}( = 90^\circ ) \)

\(\Rightarrow \widehat {ADM} = \widehat {ADN}\)

Mặt MN // BC, \(AD \bot BC \Rightarrow MN \bot AD\)

∆DMN có DA là đường cao, đường phân giác

\( \Rightarrow \Delta DMN\) cân tại D => AM = AN

Xét ∆IDC có: AM // CD \( \Rightarrow {{AM} \over {CD}} = {{AI} \over {DI}}\) (hệ quả của định lí Thales)

Xét ∆EDC có: CD // AN \( \Rightarrow {{AN} \over {CD}} = {{AE} \over {CE}}\) (hệ quả của định lí Thales) \( \Rightarrow {{AI} \over {DI}} = {{AE} \over {CE}}\)

Xét ∆AND có: \({{AI} \over {DI}} = {{AE} \over {CE}} \Rightarrow IE//AN\) (định lí Thales đảo)

Ta có IE // AN và AN // BC => IE // BC

Loigiaihay.com