Bài tập 27 trang 92 Tài liệu dạy – học Toán 8 tập 2

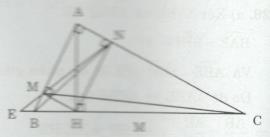
Đề bài

Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH $\left( {H \in BC} \right)$

a) Chứng minh rằng AB² = BH.BC.

b) Vẽ HM vuông góc với AB, HN vuông góc với BC. Chứng minh rằng HB.HC = AM.AB.

c) Đường thẳng MN cắt đường thẳng BC ở E. Chứng minh rằng EM.EN = EB.EC.

d) Chứng minh rằng tam giác BMN đồng dạng với tam giác MHC.

Lời giải chi tiết

a) Xét ∆ABH và ∆ABC có: góc B (chung) và $\widehat {AHB} = \widehat {BAC}( = 90^\circ )$

Do đó $\Delta ABH \sim \Delta CBA(g.g)$

$\Rightarrow {{AB} \over {BC}} = {{BH} \over {AB}}$

$\Rightarrow A{B^2} = BH.BC$

b) Xét ∆ABH và ∆AHC có:

$\widehat {BAH} = \widehat {ACH}$ (cùng phụ với góc B)

Và $\widehat {AHB} = \widehat {AHC}( = 90^\circ )$

Do đó $\Delta ABH \sim \Delta CAH(g.g)$

$\Rightarrow {{AH} \over {HC}} = {{BH} \over {AH}}$

$\Rightarrow A{H^2} = BH.HC(1)$

Xét ∆AMH và ∆ABH có: $\widehat {MAH}$ (chung) và $\widehat {AMH} = \widehat {AHB}( = 90^\circ )$

Do đó $\Delta AMH \sim \Delta AHB(g.g)$

$\Rightarrow {{AH} \over {AB}} = {{AM} \over {AH}}$

$\Rightarrow A{H^2} = AM.AB(2)$

Từ (1) và (2) suy ra: HB.HC=AM.AB

c) Xét ∆AHN và ∆AHC có: góc HAN chung và $\widehat {ANH} = \widehat {AHC}( = 90^\circ )$

Do đó $\Delta AHN \sim \Delta AHC(g.g)$

$\Rightarrow {{AH} \over {AC}} = {{AN} \over {AH}}$

$\Rightarrow A{H^2} = AN.AC$

Mà $A{H^2} = AM.AB$ (câu b) nên $AN.AC = AM.AB \Rightarrow {{AN} \over {AB}} = {{AM} \over {AC}}$

Xét ∆AMN và ∆ABC có: ${{AN} \over {AB}} = {{AM} \over {AC}}$ và $\widehat {MAN}(chung)$

Do đó $\Delta AMN \sim \Delta ACB(c.g.c)$

$\Rightarrow \widehat {AMN} = \widehat {ACB}$

Mà $\widehat {AMN} = \widehat {EMB}$ (đối đỉnh) nên $\widehat {ACB} = \widehat {EMB}$

Xét ∆ENC và ∆EBM ta có: $\widehat {MEB}$ (chung) và $\widehat {NCB} = \widehat {EMB}$ (chứng minh trên)

Do đó $\Delta ENC \sim \Delta EBM(g.g)$

$\Rightarrow {{EN} \over {EB}} = {{EC} \over {EM}}.$

Vậy EN.EM=EB.EC

d) Xét tứ giác AMHN có: $\widehat {MAN} = 90^\circ$ (∆ABC vuông tại A),

$\widehat {AMH} = 90^\circ (MH \bot AB$ tại M) và $\widehat {ANH} = 90^\circ (NH \bot AC$ tại N)

Do đó tứ giác AMHN là hình chữ nhật => MN = AH

Xét ∆BMH và ∆AHC có: $\widehat {BMH} = \widehat {AHC}( = 90^\circ )$ và $\widehat {MHB} = \widehat {ACH}$ (hai góc so lê trong và MH // AC)

Do đó $\Delta BMH \sim \Delta AHC(g.g)$

$\Rightarrow {{BM} \over {AH}} = {{MH} \over {HC}} \Rightarrow {{BM} \over {MH}} = {{AH} \over {HC}}$

Mà AH = MN nên ${{BM} \over {MH}} = {{MN} \over {HC}}$

Ta có: $\widehat {BMN} + \widehat {AMN} = 180^\circ$ (hai góc kề bù)

$\widehat {MHC} + \widehat {MHB} = 180^\circ$ (hai góc kề bù)

Và $\widehat {AMN} = \widehat {MHB}( = \widehat {ACB})$

$\Rightarrow \widehat {BMN} = \widehat {MHC}$

Xét ∆BMN và ∆MHC có: ${{BM} \over {MH}} = {{MN} \over {HC}}$ và $\widehat {BMN} = \widehat {MHC}$

Do đó $\Delta BMN \sim \Delta MHC(c.g.c)$

Loigiaihay.com