Bài tập 24 trang 92 Tài liệu dạy – học Toán 8 tập 2

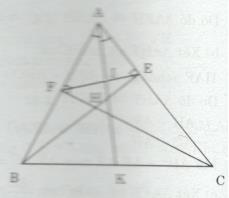
Đề bài

Cho tam giác ABC có ba góc nhọn, đường cao BE, CF cắt nhau ở H.

a) Chứng minh AE.AC = AF.AB

b) Chứng minh \(\Delta AEF \sim \Delta ABC.\)

c) Chứng minh \(\Delta HEF \sim \Delta HCB.\)

d) Phân giác của góc BAC lần lượt cắt EF tại I, cắt BC tại K.

Chứng minh \({{IE} \over {IF}} = {{KB} \over {KC}}\)

Lời giải chi tiết

a) Xét ∆ABE và ∆ACF có góc A (chung) và \(\widehat {AEB} = \widehat {AFC}( = 90^\circ )\)

Do đó \(\Delta ABE \sim \Delta ACF(g.g) \Rightarrow {{AE} \over {AF}} = {{AB} \over {AC}}\)

=> AE.AC = AF.AB

b) Ta có: \({{AE} \over {AF}} = {{AB} \over {AC}} \Rightarrow {{AE} \over {AB}} = {{AF} \over {AC}}\)

Xét ∆AEF và ∆ABC có

\({{AE} \over {AB}} = {{AF} \over {AC}}\) và góc EAF (chung)

Do đó \(\Delta AEF \sim \Delta ABC(c.g.c)\)

c) Ta có \(\widehat {AEF} = \widehat {ABC}(\Delta AEF \sim \Delta ABC)\)

Mà \(\widehat {AEF} + \widehat {HEF} = \widehat {AEB} = 90^\circ \) và \(\widehat {ABC} + \widehat {HCB} = 90^\circ \) (∆FBC vuông tại F)

Do đó \(\widehat {HEF} = \widehat {HCB}\)

Xét ∆HEF và ∆HCB có \(\widehat {HEF} = \widehat {HCB};\widehat {EHF} = \widehat {BHC}\) (đối đỉnh) \( \Rightarrow \Delta HEF \sim \Delta HCB(g.g)\)

d) ∆AEF có AI là đường phân giác (gt) nên \({{IE} \over {IF}} = {{AE} \over {AF}}\)

∆ABC có AK là đường phân giác (gt) \( \Rightarrow {{KB} \over {KC}} = {{AB} \over {AC}}\)

Ta có: \({{IE} \over {IF}} = {{AE} \over {AF}};{{KB} \over {KC}} = {{AB} \over {AC}}\) và \({{AE} \over {AF}} = {{AB} \over {AC}}\) (câu a) \( \Rightarrow {{IE} \over {IF}} = {{KB} \over {KC}}\)

Loigiaihay.com