Bài tập 23 trang 92 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Cho tam giác ABC có ba góc nhọn, đường cao AH Quảng cáo
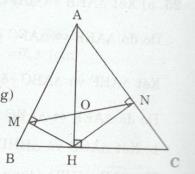
Đề bài Cho tam giác ABC có ba góc nhọn, đường cao AH \(\left( {H \in BC} \right)\). Vẽ \(HM \bot AB,\,\,HN \bot AC\,\,\)\(\left( {M \in AB,\,\,N \in AC} \right)\) a) Chứng minh rằng \(\Delta AMH \sim \Delta AHB.\) Suy ra AH2 = AM.AB. b) Chứng minh rằng AM.AB = AN.AC. c) Chứng minh \(\Delta ANM \sim \Delta ABC.\) d) Gọi O là giao điểm của AH với MN. Chứng minh OA.OH = OM.ON. Lời giải chi tiết a) Xét ∆AMH và ∆AHB có: \(\widehat {MAH}\) chung và \(\widehat {AMH} = \widehat {AHB}( = 90^\circ )\) Do đó \(\Delta AMH \sim \Delta AHB(g.g) \Rightarrow {{AH} \over {AB}} = {{AM} \over {AH}}\) \( \Rightarrow A{H^2} = AM.AB(1)\) b) Xét ∆AHN và ∆AHC có: \(\widehat {HAN}\) chung và \(\widehat {ANH} = \widehat {AHC}( = 90^\circ )\) \(\Rightarrow \Delta AHN \sim \Delta ACH(g.g)\) \( \Rightarrow {{AH} \over {AC}} = {{AN} \over {AH}} \Rightarrow A{H^2} = AN.AC(2)\) Từ (1) và (2) suy ra AM.AB = AN.AC c) Xét ∆ANM và ∆ABC có: \({{AM} \over {AC}} = {{AN} \over {AB}}\) (vì AM.AB = AN.AC) và góc MAN (chung) Do đó \(\Delta ANM \sim ABC(c.g.c)\) d) Ta có \(\widehat {AMN} = \widehat {ACB}(\Delta ANM \sim \Delta ABC)\) và \(\widehat {AHN} = \widehat {ACB}(\Delta AHN \sim \Delta ACH)\) \( \Rightarrow \widehat {AMN} = \widehat {AHN}\,hay\,\widehat {AMO} = \widehat {OHN}\) Xét ∆AMO và ∆OHN có \(\widehat {AOM} = \widehat {NOH}\) (đối đỉnh) và \(\widehat {AMO} = \widehat {OHN}\) Do đó \(\Delta AMO \sim \Delta NHO(g.g) \) \(\Rightarrow {{OA} \over {ON}} = {{OM} \over {OH}}\) \(\Rightarrow OA.OH = OM.ON\) Loigiaihay.com
|




















Danh sách bình luận