Bài tập 18 trang 91 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Cho tam giác ABC nhọn có các đường cao BE, CF cắt nhau tại H. Quảng cáo
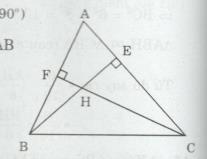
Đề bài Cho tam giác ABC nhọn có các đường cao BE, CF cắt nhau tại H. a) Chứng minh rằng tam giác AEB đồng dạng với tam giác AFC. Suy ra \(AE.AC = AF.AB.\) b) Chứng minh rằng \({{HE} \over {HC}} = {{HF} \over {HB}}\) Lời giải chi tiết a) Xét ∆AEB và ∆AFC có: \(\widehat A\) chung và \(\widehat {AEB} = \widehat {AFC}( = 90^\circ )\) \( \Rightarrow \Delta AEB \sim \Delta AFC(g.g)\) \(\Rightarrow {{AE} \over {AF}} = {{AB} \over {AC}} \Rightarrow AE.AC = AF.AB\) b) Xét ∆HEC và ∆HBF có: \(\widehat {EHC} = \widehat {BHF}\) (đối đỉnh) và \(\widehat {HEC} = \widehat {BFH}( = 90^\circ )\) \( \Rightarrow \Delta HEC \sim \Delta HFB(g.g)\) \(\Rightarrow {{HE} \over {HF}} = {{HC} \over {HB}} \Rightarrow {{HE} \over {HC}} = {{HF} \over {HB}}\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
