Bài tập 14 trang 122 Tài liệu dạy – học Toán 7 tập 2Giải bài tập Cho tam giác DEF. Tia phân giác của gióc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN. Quảng cáo
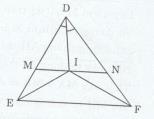
Đề bài Cho tam giác DEF. Tia phân giác của gióc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN. Lời giải chi tiết
Ta có: \(\widehat {MIE} = \widehat {IEF}\) (hai góc so le trong và MN // EF) \(\widehat {MEI} = \widehat {IEF}\) (EI là tia phân giác của \(\widehat {DEF}\)) Do đó \(\widehat {MIE} = \widehat {MEI}\) => ∆MIE cân tại M => ME = MI (1) ∆DEF có: I là giao điểm của hai đường phân giác của góc D và góc E (gt) Do đó theo định lí về ba đường phân giác Ta có FI là tia phân giác của \(\widehat {DFE}.\) \( \Rightarrow \widehat {IFE} = \widehat {IFN}\) Mà \(\widehat {IFE} = \widehat {NIF}\) (hai góc so le trong và IN // EF) Nên \(\widehat {IFN} = \widehat {NIF}.\) Do đó ∆INF cân tại N => NF = IN (2) Từ (1) và (2) cộng vế theo vế ta có: ME + NF = MI + IN = MN. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
