Bài tập 12 trang 173 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho hình bình hành ABCD có diện tích 120 m2. Gọi M và N lần lượt lã trung điểm của BC và CD. BN cắt DM tại P. Tính diện tích tứ giác ABPD. Quảng cáo
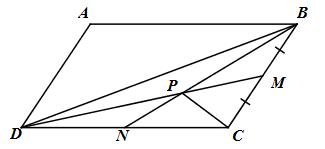
Đề bài Cho hình bình hành ABCD có diện tích 120 m2. Gọi M và N lần lượt lã trung điểm của BC và CD. BN cắt DM tại P. Tính diện tích tứ giác ABPD. Lời giải chi tiết \({S_{BCN}} = {1 \over 2}{S_{BCD}}\) (do \(CN = {1 \over 2}CD\)) và \({S_{BCD}} = {1 \over 2}{S_{ABCD}}\) (tứ giác ABCD là hình bình hành) Do đó \({S_{BCN}} = {1 \over 4}{S_{ABCD}} = {1 \over 4}.120 = 30\,\,\left( {{m^2}} \right)\) Tương tự: \({S_{DCM}} = 30\,\,\left( {{m^2}} \right)\) \({S_{BCN}} = S{ _{DCM}} \Rightarrow {S_{DNP}} + {S_{CMPN}} \)\(\;= {S_{BMP}} + {S_{CMPN}}\)
\( \Rightarrow {S_{DNP}} = {S_{BMP}}\) Mặt khác \({S_{BMP}} = {S_{CMP}}\,\,\left( {BM = CM} \right),\) \({S_{DNP}} = {S_{CPN}}\,\,\left( {DN = CN} \right)\) Do đso \({S_{BMP}} = {S_{CMP}} = {S_{CPN}} = 30:3 = 10\,\,\left( {{m^2}} \right)\) Do vậy \({S_{ABPD}} = {S_{ABCD}} - {S_{DCM}} - {S_{BMP}} \)\(\,= 120 - 30 - 10 = 80\,\,\left( {{m^2}} \right)\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
