Bài 97 trang 121 SBT Hình học 10 Nâng caoGiải bài tập Bài 97 trang 121 SBT Hình học 10 Nâng cao Quảng cáo
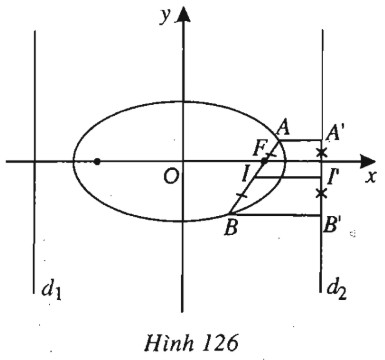
Đề bài Một đường thẳng đi qua tiêu điểm \(F(c ; 0)\) của elip \((E): \dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) \((a>b>0)\) và cắt nó tại hai điểm \(A, B\). Chứng minh rằng đường tròn đường kính \(AB\) không có điểm chung với đường chuẩn :\(x = \dfrac{a}{e}\). Lời giải chi tiết (h.126).
Gọi \(I\) là trung điểm của \(AB; A’, B’, I’\) lần lượt là hình chiếu của \(A, B, I\) trên đường chuẩn \({d_2}: x = \dfrac{{{a^2}}}{c}\). Ta sẽ chứng minh: \(II' > \dfrac{{AB}}{2} \Leftrightarrow AA' + BB' > AB\). Ta có \(AB = AF + BF = e.AA' + e.BB' \) \(= e(AA' + BB') < AA' + BB' = 2II'\) (do \(e<1\)). Suy ra điều cần chứng minh. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
