Bài 91 trang 52 SBT Hình học 10 Nâng cao

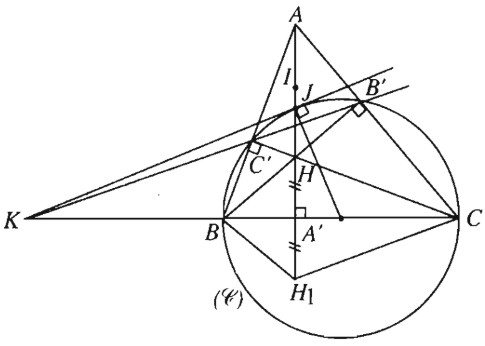
Đề bài

Trong tam giác \(ABC\) kẻ các đường cao \(AA’, BB’, CC’\) và gọi \(H\) là trực tâm của tam giác.

a) Chứng minh

\(\overrightarrow {A'B} .\overrightarrow {A'C}  =  - \overrightarrow {A'H} .\overrightarrow {A'A}. \)

b) Gọi \(J\) là một giao điểm của \(AA’\) với đường tròn \((C)\) đường kính \(BC\). Chứng minh rằng các đường thẳng \(BC, B’C’\) và tiếp tuyến tại \(J\) của \((C)\) đồng quy.

Lời giải chi tiết

(h.78).

 

a) Lấy điểm \(H_1\) đối xứng với \(H\) qua \(A’\) hay \(\overrightarrow {A'H}  =  - \overrightarrow {A'{H_1}} \).

Khi đó, \(\widehat {B{H_1}C} = \widehat {BHC} = \widehat {B'HC'} = {180^0} - \widehat A\).

Suy ra \(ABH_1C\) là tứ giác nội tiếp, do đó

\(\overrightarrow {A'B} .\overrightarrow {A'C}  = \overrightarrow {A'{H_1}.} \overrightarrow {A'A}  =  - \overrightarrow {A'H} .\overrightarrow {A'A} \).

b) Đường tròn \((C)\) và đường tròn tâm \(I\) đường kính \(HA\) có \(B’C’\) là trục đẳng phương. Kẻ tiếp tuyến của \((C)\) tại \(J\) cắt đường thẳng \(BC\) ở \(K\) thì \(K{J^2} = \overrightarrow {KB} .\overrightarrow {KC}  = {\wp _{K/(C)}}\).

Ta hãy tính phương tích của \(K\) đối với đường tròn tâm \(I\):

\(\begin{array}{l}{\wp _{K/(I)}} = K{I^2} - {\left( {\dfrac{{AH}}{2}} \right)^2}\\ = KA{'^2} + {\overrightarrow {A'I} ^2} - {\left( {\dfrac{{\overrightarrow {AH} }}{2}} \right)^2}\\              = KA{'^2} + {\left( {\dfrac{{\overrightarrow {A'A}  + \overrightarrow {A'H} }}{2}} \right)^2} - {\left( {\dfrac{{\overrightarrow {A'H}  - \overrightarrow {A'A} }}{2}} \right)^2}\\              = KA{'^2} + \overrightarrow {A'H} .\overrightarrow {A'A} \end{array}\)

Theo câu a), \(\overrightarrow {A'H} .\overrightarrow {A'A}  =  - \overrightarrow {A'B} .\overrightarrow {A'C} \).

Mặt khác , ta có \(\widehat {BJC} = {90^0}\) ( góc nội tiếp chắn nửa đường tròn) và \(JA' \bot BC\) nên \(A'{J^2} =  - \overrightarrow {A'B} .\overrightarrow {A'C} \).

Vậy \({\wp _{K/(I)}} = KA{'^2} + A'{J^2} = K{J^2} = {\wp _{K/(C)}}\), suy ra \(K\) thuộc trục đẳng phương \(B’C’\). Vậy ba đường thẳng \(BC, B’C’\) và tiếp tuyến tại \(J\) của \((C)\) đồng quy ở \(K\).

Loigiaihay.com