Bài 88 trang 51 SBT Hình học 10 Nâng cao

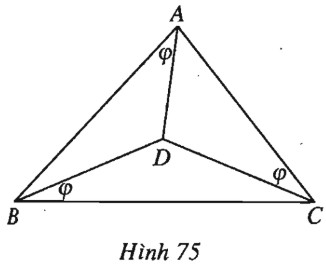
Đề bài

Cho điểm \(D\) nằm trong tam giác \(ABC\) sao cho \(\widehat {DAB} = \widehat {DBC} = \widehat {DCA} = \varphi .\) Chứng minh rằng:

a) \({\sin ^3}\varphi  = \sin (A - \varphi )\)\(.\sin (B - \varphi ).\sin (C - \varphi ).\)

b) \(\cot \varphi  = \cot A + \cot B + \cot C.\)

Lời giải chi tiết

(h.75).

a) Theo định lí sin, trong tam giác \(ABD\) ta có

\(\dfrac{{DB}}{{\sin \varphi }} = \dfrac{{AD}}{{\sin (B - \varphi )}}\) ,     (1)

trong tam giác BCD có

\(\dfrac{{CD}}{{\sin \varphi }} = \dfrac{{BD}}{{\sin (C - \varphi )}}\),      (2)

trong tam giác \(ACD\) có

\(\dfrac{{AD}}{{\sin \varphi }} = \dfrac{{CD}}{{\sin (A - \varphi )}}\).

Từ đó ta có

\(\dfrac{{AD.BD.CD}}{{{{\sin }^3}\varphi }}\)

\(= \dfrac{{AD.BD.CD}}{{\sin (A - \varphi )\sin (B - \varphi )\sin (C - \varphi )}}\).

Suy ra đẳng thức cần chứng minh.

b) Áp dụng định lí cosin vào tam giác \(DAB\) ta có

\(B{D^2}\)\( = A{B^2} + A{D^2} - 2.AB.AD.\cos \varphi. \)

Mặt khác, \(\dfrac{1}{2}AB.AD.\sin \varphi  = {S_{ABD}}\) .

Từ đó suy ra \(B{D^2} = A{B^2} + A{D^2} - 4{S_{ABD}}.\cot \varphi \).

Tương tự ta cũng có \(C{D^2} = B{C^2} + B{D^2} - 4{S_{DBC}}.\cot \varphi  ;\) \(  A{D^2} = A{C^2} + C{D^2} - 4{S_{DCA}}.\cot \varphi. \)

Cộng theo vế rồi biến đổi, chú ý rằng tổng diện tích ba tam giác nhỏ bằng diện tích \(S\) của tam giác \(ABC\), ta được

\(\cot \varphi  = \dfrac{{{a^2} + {b^2} + {c^2}}}{{4S}}\) \( = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R.\)

Theo bài 58 chương II, \(\cot A + \cot B + \cot C\) \( = \dfrac{{{a^2} + {b^2} + {c^2}}}{{abc}}R.\)

Từ đó suy ra đẳng thức cần chứng minh.

Loigiaihay.com