Bài 86 trang 51 SBT Hình học 10 Nâng caoGiải bài tập Bài 86 trang 51 SBT Hình học 10 Nâng cao Quảng cáo
Đề bài Cho tam giác \(ABC\) có \(\widehat A = {60^0} , a = 10 , r = \dfrac{{5\sqrt 3 }}{3}\). a) Tính \(R.\) b) Tính \(b, c.\) Lời giải chi tiết
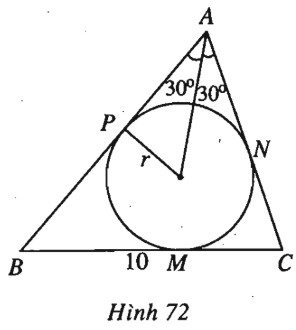
a) Ta có \(2R = \dfrac{a}{{\sin A}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3} \) \( \Rightarrow R = \dfrac{{10\sqrt 3 }}{3}\). b) Gọi \(M, N, P\) lần lượt là các tiếp điểm của \(BC, CA, AB\) với đường tròn nội tiếp tam giác \(ABC\) (h.72). Ta có \(AP = AN = r.\cot {30^0} = 5 ; \) \(BP + NC = BM + MC = a = 10\). Từ đó ta có \((b - AN) + (c - AP) = 10\) hay \(b+c=20.\) (1) Theo định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos {60^0}\) hay \({a^2} = {(b + c)^2} - 2bc - bc\), suy ra \(bc = \dfrac{{{{(b + c)}^2} - {a^2}}}{3}\) \( = \dfrac{{{{20}^2} - {{10}^2}}}{3} = 100\) (2) Từ (1) và (2) suy ra \(b, c\) là nghiệm của phương trình bậc hai \({x^2} - 20x + 100 = 0\). Phương trình này có nghiệm kép \(b=c=10\) nên \(ABC\) là tam giác đều. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
