Bài 9 trang 94 Tài liệu dạy – học Toán 9 tập 2

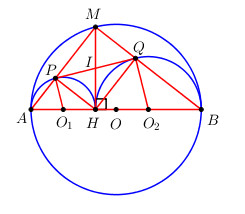
Đề bài

Cho đường tròn tâm (O) có đường kính AB. M là một điểm tùy ý trên đường tròn không trùng với A và B. Vẽ MH vuông góc với AB tại H. Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (O), vẽ hai nửa đường tròn đường kính HA và HB có tâm lần lượt là O₁ và O₂. MA và MB cắt hai nửa đường tròn lần lượt tại P và Q.

a) Chứng minh MH = PQ. Tính độ dài đoạn PQ theo AH = a và BH = b.

b) Chứng minh PQ tiếp xúc với hai đường tròn (O₁) và (O₂).

c) Xác định vị trí điểm M sao cho MPHQ là một hình vuông.

Lời giải chi tiết

 

a) Ta có \(\widehat {APH} = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( {{O_1}} \right)\)) \( \Rightarrow PH \bot AM\).

\(\widehat {BQH} = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( {{O_2}} \right)\)) \( \Rightarrow HQ \bot BM\)

\(\widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)\))

Xét tứ giác MPHQ có: \(\widehat {PMQ} = \widehat {HPM} = \widehat {HQM} = {90^0}\) \( \Rightarrow MPHQ\) là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow MH = PQ\) (hai đường chéo của hình chữ nhật).

Áp dụng hệ thức lượng trong tam giác vuông ABM có: \(M{H^2} = AH.BH = ab \Rightarrow MH = \sqrt {ab} \).

Mà \(MH = PQ\,\,\left( {cmt} \right) \Rightarrow PQ = \sqrt {ab} \).

b) Gọi I là giao điểm của MH và PQ. Do MPHQ là hình chữ nhật \( \Rightarrow IP = IH \Rightarrow \Delta IPH\) cân tại I \( \Rightarrow \widehat {IPH} = \widehat {IHP}\)  (1).

Lại có \({O_1}P = {O_1}H\) (do H, P cùng thuộc đường tròn \(\left( {{O_1}} \right)\)) \( \Rightarrow \Delta {O_1}PH\) cân tại \({O_1} \Rightarrow \widehat {{O_1}PH} = \widehat {{O_1}HP}\)   (2)

Từ (1) và (2) \( \Rightarrow \widehat {IPH} + \widehat {{O_1}PH} = \widehat {IHP} + \widehat {{O_1}HP} \) \(\Leftrightarrow \widehat {{O_1}PI} = \widehat {{O_1}HI}\)

Mà \(MH \bot AB \Rightarrow \widehat {{O_1}HI} = {90^0}\) \( \Rightarrow \widehat {{O_1}PI} = {90^0} \) \(\Rightarrow {O_1}P \bot PQ\) tại P.

\( \Rightarrow PQ\) là tiếp tuyến của đường tròn \(\left( {{O_1}} \right)\) tại P.

Hoàn toàn tương tự ta chứng minh được \(\widehat {{O_2}QI} = {90^0} \Rightarrow {O_2}Q \bot PQ \Rightarrow PQ\) là tiếp tuyến của đường tròn \(\left( {{O_2}} \right)\) tại Q.

Vậy PQ tiếp xúc với hai đường tròn (O₁) và (O₂).

c) Hình chữ nhật MPHQ cần thêm điều kiện MH là tia phân giác của \(\widehat {PMQ}\) sẽ trở thành hình vuông.

Khi MH là phân giác của \(\widehat {PMQ}\) thì tam giác ABC có đường cao MH đồng thời là phân giác \( \Rightarrow \Delta AMB\) cân tại M  (hai dây bằng nhau căng hai cung bằng nhau).

Vậy M là điểm chính giữa cung AB.

 Loigiaihay.com