Bài 13 trang 95 Tài liệu dạy – học Toán 9 tập 2

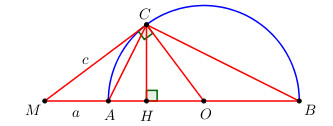
Đề bài

Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với đường tròn. Gọi H là hình chiếu của C trên AB.

a) Chứng minh rằng CA là phân giác của góc \(\widehat {MCH}\).

b) Giả sử MA = a, MC = c, tính AB và CH.

Lời giải chi tiết

 

a) Ta có \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại C

\( \Rightarrow \widehat {ABC} + \widehat {BAC} = {90^0}\) (hai góc nhọn trong tam giác vuông) hay \(\widehat {ABC} + \widehat {HAC} = {90^0}\)

\(\Delta AHC\) vuông tại H \( \Rightarrow \widehat {HAC} + \widehat {ACH} = {90^0}\) (hai góc nhọn trong tam giác vuông).

\( \Rightarrow \widehat {ABC} = \widehat {ACH}\) (cùng phụ với\(\widehat {HAC}\))

Lại có \(\widehat {ACM} = \widehat {ABC}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC)

\( \Rightarrow \widehat {ACM} = \widehat {ACH} \Rightarrow CA\) là tia phân giác của \(\widehat {MCH}\).

b) Gọi bán kính của đường tròn đường kính AB là R

Áp dụng định lí Pytago trong tam giác vuông OCM có :

\(\begin{array}{l}M{C^2} + O{C^2} = O{M^2} \\\Leftrightarrow {c^2} + {R^2} = {\left( {a + R} \right)^2}\\ \Leftrightarrow {c^2} + {R^2} = {a^2} + 2aR + {R^2} \\\Leftrightarrow {a^2} + 2Ra - {c^2} = 0\\ \Leftrightarrow 2R = \dfrac{{{c^2} - {a^2}}}{a} = AB \\\Rightarrow R = \dfrac{{{c^2} - {a^2}}}{{2a}}\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông OCM có :

\(\begin{array}{l}\dfrac{1}{{C{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{C{M^2}}}\\ \Leftrightarrow \dfrac{1}{{C{H^2}}} = \dfrac{1}{{{R^2}}} + \dfrac{1}{{{c^2}}}\\ \Leftrightarrow \dfrac{1}{{C{H^2}}} = \dfrac{{4{a^2}}}{{{c^2} - {a^2}}} + \dfrac{1}{{{c^2}}}\\ \Leftrightarrow \dfrac{1}{{C{H^2}}} = \dfrac{{4{a^2}{c^2} + {c^2} - {a^2}}}{{{c^2}\left( {{c^2} - {a^2}} \right)}}\\ \Rightarrow C{H^2} = \dfrac{{{c^2}\left( {{c^2} - {a^2}} \right)}}{{4{a^2}{c^2} + {c^2} - {a^2}}}\\ \Rightarrow CH = \sqrt {\dfrac{{{c^2}\left( {{c^2} - {a^2}} \right)}}{{4{a^2}{c^2} + {c^2} - {a^2}}}} \end{array}\)

 Loigiaihay.com