Bài 9 trang 17 SGK Hình học 10

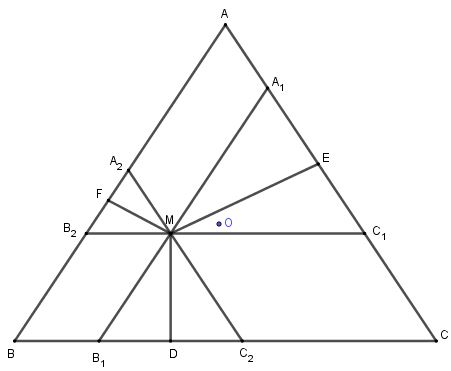
Đề bài

Cho tam giác đều $ABC$ có trọng tâm $O$ và $M$ là một điểm tùy ý trong tam giác. Gọi $D,E,F$ lần lượt là chân đường vuông góc hạ từ $M$ đến $BC, AC, AB$. Chứng minh rằng:

$\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF}  = {3 \over 2}\overrightarrow {MO}$

Lời giải chi tiết

+) Qua $M$ kẻ các đường ${A_1}{B_1}\;//{\rm{ }}AB;{\rm{ }}{A_2}{C_2}\;//{\rm{ }}AC;{\rm{ }}{B_2}{C_1}\;//{\rm{ }}BC$ như hình vẽ.

Ta có:

$\begin{array}{l} M{B_1}//AB \Rightarrow \widehat {M{B_1}{C_2}} = \widehat {ABC} = {60^0}\\ M{C_2}//AC \Rightarrow \widehat {M{C_2}{B_1}} = \widehat {ACB} = {60^0} \end{array}$

Tam giác $M{B_1}{C_2}$ có $\widehat {M{B_1}{C_2}} = \widehat {M{C_2}{B_1}} = {60^0}$ nên là tam giác đều.

Tương tự các tam giác $M{A_1}{C_1};M{A_2}{B_2}$đều là các tam giác đều.

+) Lại có $MD\; \bot {B_1}{C_2}$ nên $MD$ cũng là trung tuyến của tam giác ${B_1}D{C_2}$

Ta có $2\overrightarrow {MD}  = \overrightarrow {M{B_1}}  + \overrightarrow {M{C_2}}$

Tương tự: $2\overrightarrow {ME}  = \overrightarrow {M{A_1}}  + \overrightarrow {M{C_1}}$

               $2\overrightarrow {MF}  = \overrightarrow {M{A_2}}  + \overrightarrow {M{B_2}}$

$\begin{array}{l} \Rightarrow 2\overrightarrow {MD} + 2\overrightarrow {ME} + 2\overrightarrow {MF} \\ = \left( {\overrightarrow {M{B_1}} + \overrightarrow {M{C_2}} } \right) \\+ \left( {\overrightarrow {M{C_1}} + \overrightarrow {M{A_1}} } \right) \\+ \left( {\overrightarrow {M{A_2}} + \overrightarrow {M{B_2}} } \right) \end{array}$

$\Rightarrow 2\left( {\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF} } \right)$

$= \left( {\overrightarrow {M{A_1}}  + \overrightarrow {M{A_2}} } \right) + \left( {\overrightarrow {M{B_1}}  + \overrightarrow {M{B_2}} } \right) + \left( {\overrightarrow {M{C_1}}  + \overrightarrow {M{C_2}} } \right)$

+) Mặt khác: Tứ giác $M{A_1}A{A_2}$ là hình bình hành nên  $\overrightarrow {M{A_1}}  + \overrightarrow {M{A_2}}  = \overrightarrow {MA}$

Tương tự: $\overrightarrow {M{B_1}}  + \overrightarrow {M{B_2}}  = \overrightarrow {MB} ;\quad \overrightarrow {M{C_1}}  + \overrightarrow {M{C_2}}  = \overrightarrow {MC}$

$\Rightarrow 2\left( {\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF} } \right) = \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} {\rm{ }}$

Vì $O$ là trọng tâm của tam giác và $M$ là một điểm bất kì nên

$\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MO}$

+) Cuối cùng ta có: 

$\Rightarrow 2\left( {\overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF} } \right) = 3\overrightarrow {MO}$

$\Rightarrow \overrightarrow {MD}  + \overrightarrow {ME}  + \overrightarrow {MF}  = \frac{3}{2}\overrightarrow {MO}$

Loigiaihay.com