Bài 9 trang 114 SGK Hình học 11

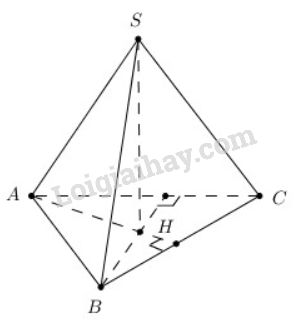
Đề bài

Cho hình chóp tam giác đều \(S.ABC \) có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\).

Lời giải chi tiết

Hình chóp tam giác đều nên ta có \(H\) là tâm của tam giác đều \(ABC\)

\(SH ⊥ (ABC) \Rightarrow SH ⊥ BC\)

Và \(AH ⊥ BC\) (vì \(H\) là trực tâm)

Suy ra \( BC ⊥ (SAH)\)

\(SA\subset (SAH)\Rightarrow BC ⊥ SA\).

Chứng minh tương tự, ta có:

\(SH \, \bot  \, \left( {ABC} \right) \Rightarrow SH \,  \bot  \, AC\).

Mà \(H\) là trực tâm của tam giác \(ABC\) \( \Rightarrow BH \,  \bot  \, AC\)

\( \Rightarrow AC \,  \bot \,  \left( {SBH} \right);\,\,SB \subset \left( {SBH} \right) \) \(\Rightarrow AC \,  \bot  \, SB\)

Cách khác:

Sử dụng định lí ba đường vuông góc

+ Ta có: \(AH ⊥ BC\)

Mà \(AH\) là hình chiếu của \(SA\) trên \((ABC)\)

\(⇒ BC ⊥ SA\) ( định lí ba đường vuông góc)

+ Lại có : \(AC ⊥ BH.\)

\(BH\) là hình chiếu của \(SB\) trên \((ABC)\)

\(⇒ AC ⊥ SB\) ( định lí ba đường vuông góc)

 Loigiaihay.com