Bài 85 trang 51 SBT Hình học 10 Nâng cao

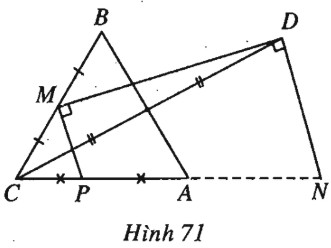
Đề bài

Cho tam giác đều \(BAC\) có cạnh bằng \(1\). Gọi \(D\) là điểm đối xứng với \(C\) qua đường thẳng \(AB, M\) là trung điểm của cạnh \(CB.\)

a) Xác định trên đường thẳng \(AC\) một điểm \(N\) sao cho tam giác \(MDN\) vuông tại \(D\). Tính diện tích tam giác đó.

b) Xác định trên đường thẳng \(AC\) điểm \(P\) sao cho tam giác \(MPD\) vuông tại \(M\). Tính diện tích tam giác đó.

c) Tính côsin của góc hợp bởi hai đường thẳng \(MP\) và \(PD.\)

Lời giải chi tiết

(h.71).

Đặt \(\overrightarrow {CA}  = \overrightarrow a   ;  \overrightarrow {CB}  = \overrightarrow b \).

Khi đó \(\overrightarrow {CD}  = \overrightarrow a  + \overrightarrow b  ;  \overrightarrow {CM}  = \dfrac{{\overrightarrow b }}{2}  ;\) \(  {\overrightarrow a ^2} = {\overrightarrow b ^2} = 1 ;  \overrightarrow a .\overrightarrow b  = \dfrac{1}{2}\).

a) Giả sử \(\overrightarrow {CN}  = n\overrightarrow {CA}  = n\overrightarrow a \). Khi đó ta có

\(\overrightarrow {MD}  = \overrightarrow {CD}  - \overrightarrow {CM}  = \overrightarrow a  + \dfrac{{\overrightarrow b }}{2} ;\) \(  \overrightarrow {ND}  = \overrightarrow {CD}  - \overrightarrow {CN}  = (1 - n)\overrightarrow a  + \overrightarrow b \).

Suy ra\(\begin{array}{l}\overrightarrow {MD} .\overrightarrow {ND}  = \left( {\overrightarrow a  + \dfrac{{\overrightarrow b }}{2}} \right)\left[ {(1 - n)\overrightarrow a  + \overrightarrow b } \right]\\                    = (1 - n){\overrightarrow a ^2} + \dfrac{{{{\overrightarrow b }^2}}}{2} + \left( {1 + \dfrac{{1 - n}}{2}} \right)\overrightarrow a .\overrightarrow b \\                    = 1 - n + \dfrac{1}{2} + \dfrac{{3 - n}}{4} = \dfrac{{9 - 5n}}{4}.\end{array}\)

Để tam giác MDN vuông tại D ta phải có \(\overrightarrow {MD} .\overrightarrow {ND}  = \overrightarrow 0 \) hay \(n = \dfrac{9}{5}\).

Vậy \(\overrightarrow {CN}  = \dfrac{9}{5}\overrightarrow a \).

Để tính diện tích tam giác MDN, ta tính bình phương độ dài hai cạnh MD và ND :

\(\begin{array}{l}M{D^2} = {\overrightarrow {MD} ^2} = {\left( {\overrightarrow a  + \dfrac{{\overrightarrow b }}{2}} \right)^2}\\ = 1 + \dfrac{1}{4} + \dfrac{1}{2} = \dfrac{7}{4}.\\N{D^2} = {\overrightarrow {ND} ^2} = {\left( { - \dfrac{4}{5}\overrightarrow a  + \overrightarrow b } \right)^2}\\ = \dfrac{{16}}{{25}} + 1 - \dfrac{4}{5} = \dfrac{{21}}{{25}}.\end{array}\).

Vậy \({S_{MDN}} = \dfrac{1}{2}\sqrt {\dfrac{7}{4}.\dfrac{{21}}{{25}}}  = \dfrac{{7\sqrt 3 }}{{20}}\).

b) Giả sử \(\overrightarrow {CP}  = p\overrightarrow {CA}  = p\overrightarrow a \). Ta có \(\overrightarrow {MP}  = \overrightarrow {CP}  - \overrightarrow {CM}  = p\overrightarrow a  - \dfrac{1}{2}\overrightarrow b \).

Khi đó \(\overrightarrow {MD} .\overrightarrow {MP}  = \left( {\overrightarrow a  + \dfrac{{\overrightarrow b }}{2}} \right)\left( {p\overrightarrow a  - \dfrac{{\overrightarrow b }}{2}} \right) \\= p - \dfrac{1}{4} - \dfrac{1}{4} + \dfrac{p}{4} = \dfrac{{5p - 2}}{4}.\)

Để tam giác PMD vuông tại M ta phải có \(\overrightarrow {MD} .\overrightarrow {MP}  = \overrightarrow 0 \) hay \(p = \dfrac{2}{5}\), tức \(\overrightarrow {CP}  = \dfrac{2}{5}\overrightarrow a \).

Khi đó \(M{P^2} = {\overrightarrow {MP} ^2} = {\left( {\dfrac{2}{5}\overrightarrow a  - \dfrac{{\overrightarrow b }}{2}} \right)^2}\\ = \dfrac{4}{{25}} + \dfrac{1}{4} - \dfrac{1}{5} = \dfrac{{21}}{{100}}.\)

Vậy \({S_{PMD}} = \dfrac{1}{2}\sqrt {\dfrac{{21}}{{100}}.\dfrac{7}{4}}  = \dfrac{{7\sqrt 3 }}{{40}}\).

c) Theo trên, ta có \(\overrightarrow {MP}  = \dfrac{{2\overrightarrow a }}{5} - \dfrac{{\overrightarrow b }}{2} ; \)

\( \overrightarrow {PD}  = \overrightarrow {CD}  = \overrightarrow {CP} \)

\(= \overrightarrow a  + \overrightarrow b  - \dfrac{2}{5}\overrightarrow a  = \dfrac{3}{5}\overrightarrow a  + \overrightarrow b \).

Bởi vậy

\(\begin{array}{l}{\overrightarrow {MP} ^2} = \dfrac{4}{{25}} + \dfrac{1}{4} - \dfrac{1}{5} = \dfrac{{21}}{{100}} ; \\ {\overrightarrow {PD} ^2} = \dfrac{9}{{25}} + 1 + \dfrac{3}{5} = \dfrac{{49}}{{25}}.\\\overrightarrow {MP} .\overrightarrow {PD}  = \dfrac{6}{{25}} + \dfrac{1}{5} - \dfrac{3}{{20}} - \dfrac{1}{2}\\ =  - \dfrac{{21}}{{100}}.\end{array}\)

Gọi \(\alpha \) là góc hợp bởi hai đường thẳng MP và PD ta có

\(\cos \alpha  = \dfrac{{|\overrightarrow {MP} .\overrightarrow {PD} |}}{{|\overrightarrow {MP} |.|\overrightarrow {PD} |}}\\ = \dfrac{{21}}{{100}}:\left( {\sqrt {\dfrac{{21}}{{100}}} .\sqrt {\dfrac{{49}}{{25}}} } \right)\\ = \dfrac{{\sqrt {21} }}{{10}}.\dfrac{5}{7} = \dfrac{{\sqrt {21} }}{{14}}\).

Loigiaihay.com