Bài 83 trang 116 SBT Hình học 10 Nâng cao

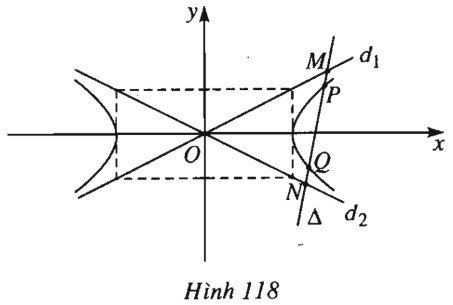
Đề bài

Cho hypebol \((H):  \dfrac{{{x^2}}}{{{a^2}}} -  \dfrac{{{y^2}}}{{{b^2}}} = 1\). Một đường thẳng \(\Delta \) cắt \((H)\) tại \(P, Q\) và hai đường tiệm cận ở \(M\) và \(N\). Chứng minh rằng

a) \(MP=NQ ;\)

b) Nếu \(\Delta \) có phương không đổi thì tích \(\overline {PM} .\overline {PN} \)là hằng số.

Lời giải chi tiết

(h.118).

a) Phương trình \((H) : \dfrac{{{x^2}}}{{{a^2}}} -  \dfrac{{{y^2}}}{{{b^2}}} = 1\).

Phương trình chung của các đường tiệm cận \(d_1, d_2\) là \( \dfrac{{{x^2}}}{{{a^2}}} -  \dfrac{{{y^2}}}{{{b^2}}} = 0\).

Gọi phương trình của \(\Delta \) là: \(\alpha x + \beta y + \gamma  = 0   ({\alpha ^2} + {\beta ^2} \ne 0)\).

Giả sử \(\beta  \ne 0\) , khi đó, do vế trái của phương trình \((H)\) và phương trình các đường tiệm cận giống nhau nên:

- Hoành độ các giao điểm \(P\) và \(Q\) của \(\Delta \) và \((H)\) là nghiệm của phương trình dạng:

\(a{x^2} + bx + c = 0\).

- Hoành độ các giao điểm \(M\) và \(N\) của \(\Delta \) và các tiệm cận là nghiệm của phương trình dạng:

\(a{x^2} + bx + d = 0\).

Gọi \(I, J\) lần lượt là trung điểm của \(PQ\) và \(MN,\) thì ta có: \({x_I} = {x_J} =  -  \dfrac{b}{{2a}}\). Suy ra \(I\) trùng với \(J\). Vậy \(MP=NQ.\)

Nếu \(\beta  = 0\) thì \(\Delta \) là đường thẳng vuông góc với \(Ox\). Vì \((H)\) và hai đường tiệm cận đều nhận \(Ox\) làm trục đối xứng nên dễ có \(MP=NQ.\)

b) Gọi \(\overrightarrow u (m ; n)  ({m^2} + {n^2} \ne 0)\) là vec tơ chỉ phương của \(\Delta \) và kí hiệu \(P = ({x_0} ; {y_0})\). Khi đó tồn tại các số \(t_1, t_2\) sao cho \(\overrightarrow {PM}  = {\kern 1pt} {t_1}\overrightarrow u  ,  \overrightarrow {PN}  = {t_2}\overrightarrow u \).

Ta có tọa độ của \(M\) và \(N\) là \(\left\{ \begin{array}{l}{x_M} = {x_0} + {t_1}m\\{y_M} = {y_0} + {t_1}n\end{array} \right.  ,   \left\{ \begin{array}{l}{x_N} = {x_0} + {t_2}m\\{y_N} = {y_0} + {t_2}n.\end{array} \right.\)

\(M , N\) thuộc hai tiệm cận của \((H)\) nên \(t_1, t_2\) là nghiệm của phương trình:

\( \dfrac{{{{({x_0} + tm)}^2}}}{{{a^2}}} -  \dfrac{{{{({y_0} + tn)}^2}}}{{{b^2}}} = 0\) hay \(\left( { \dfrac{{{m^2}}}{{{a^2}}} -  \dfrac{{{n^2}}}{{{b^2}}}} \right){t^2} + 2\left( { \dfrac{{{x_0}m}}{{{a^2}}} -  \dfrac{{{y_0}n}}{{{b^2}}}} \right)t + 1 = 0.\)

Rõ ràng \( \dfrac{{{m^2}}}{{{a^2}}} -  \dfrac{{{n^2}}}{{{b^2}}} \ne 0\).

Do đó \({t_1}.{t_2} =  \dfrac{1}{{ \dfrac{{{m^2}}}{{{a^2}}} -  \dfrac{{{n^2}}}{{{b^2}}}}} =  \dfrac{{{a^2}{b^2}}}{{{m^2}{b^2} - {n^2}{a^2}}}\).

Vậy \(\overline {PM} .\overline {PN}  = \overrightarrow {PM} .\overrightarrow {PN} \)

\(= {t_1}.{t_2}.{\overrightarrow u ^2} =  \dfrac{{{a^2}{b^2}}}{{{m^2}{b^2} - {n^2}{a^2}}}.({m^2} + {n^2})\) không đổi.

Loigiaihay.com