Bài 80 trang 155 SGK Đại số 10 nâng caoVới giá trị nào của m, bất phương trình: Quảng cáo
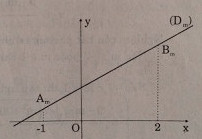
Đề bài Với giá trị nào của m, bất phương trình: (m2 + 1)x + m(x + 3) + 1 > 0 nghiệm đúng ∀x ∈ [-1; 2] ? Phương pháp giải - Xem chi tiết Tìm tập nghiệm S của bpt đã cho. BPT nghiệm đúng với mọi x thuộc [-1;2] nếu \(\left[ { - 1;2} \right] \subset S\). Lời giải chi tiết Ta có: \(\begin{array}{l}\left( {{m^2} + 1} \right)x + m\left( {x + 3} \right) + 1 > 0\\ \Leftrightarrow \left( {{m^2} + 1} \right)x + mx + 3m + 1 > 0\\ \Leftrightarrow \left( {{m^2} + m + 1} \right)x > - 3m - 1\\ \Leftrightarrow x > \frac{{ - 3m - 1}}{{{m^2} + m + 1}}\end{array}\) (Vì \({m^2} + m + 1 \) \(= {\left( {m + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall m\)) Tập nghiệm của bpt là \(S = \left( {\frac{{ - 3m - 1}}{{{m^2} + m + 1}}; + \infty } \right)\) Để bpt nghiệm đúng với mọi \(x \in \left[ { - 1;2} \right]\) thì \(\begin{array}{l}\left[ { - 1;2} \right] \subset S\\ \Leftrightarrow \frac{{ - 3m - 1}}{{{m^2} + m + 1}} < - 1\\ \Leftrightarrow - 3m - 1 < - {m^2} - m - 1\\\left( {Do\,{m^2} + m + 1 > 0} \right)\\ \Leftrightarrow {m^2} - 2m < 0\\ \Leftrightarrow 0 < m < 2\end{array}\) Cách khác: Ta có: (m2 +1)x + m.(x+3)+ 1> 0 ⇔ (m2 + 1) x +mx + 3m +1 >0 ⇔ (m2 +1+ m). x+ 3m + 1 > 0 Đặt y = f(x) = (m2 + m + 1)x+ 3m + 1 Ta coi y =f(x) là hàm số ẩn x và tham số m. Đồ thị của hàm số y = f(x) là đường thẳng (Dm ). Gọi Am và Bm là các điểm trên đường thẳng (Dm) có hoành độ theo thứ tự là -1 và 2.
f(x) > 0 với ∀x ∈ [-1; 2] khi và chỉ khi đoạn thẳng AmBm nằm phía trên trục hoành. Điều này xảy ra khi và chỉ khi Am và Bm nằm phía trên trục hoành, tức là: \(\left\{ \matrix{ Mà \(f\left( { - 1} \right) = \left( {{m^2} + m + 1} \right).\left( { - 1} \right) + 3m + 1\)\( = - {m^2} + 2m\) \(f\left( 2 \right) = \left( {{m^2} + m + 1} \right).2 + 3m + 1\)\( = 2{m^2} + 5m + 3\) Nên \(\left\{ \begin{array}{l} - {m^2} + 2m > 0\\2{m^2} + 5m + 3 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}0 < m < 2\\\left[ \begin{array}{l}m > - 1\\m < - \frac{3}{2}\end{array} \right.\end{array} \right. \Leftrightarrow 0 < m < 2\) Vậy \(0 < m < 2\). Loigiaihay.com
|




















Danh sách bình luận