Bài 8 trang 8 SGK Đại số và Giải tích 12 Nâng caoChứng minh các bất đẳng thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Chứng minh các bất đẳng thức sau: LG a \(\sin x < x\) với mọi \(x > 0,\sin x > x\) với mọi \(x < 0\) Lời giải chi tiết: Xét hàm số \(f\left( x \right) = x - \sin x\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) Đạo hàm \(f'\left( x \right) = 1 - \cos x > 0\) với mọi \(x \in \left( {0;{\pi \over 2}} \right)\). Do đó hàm số đồng biến trên \(\left[ {0;{\pi \over 2}} \right)\) Từ đó với mọi \(x \in \left( {0;{\pi \over 2}} \right)\) ta có: \(f\left( x \right) > f\left( 0 \right) = 0 \) \(\Rightarrow x - \sin x > 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right)\). \( \Leftrightarrow x > \sin x,\forall x \in \left( {0;\frac{\pi }{2}} \right)\) Với \(x \ge {\pi \over 2}\) thì \(x > 1 \ge \sin x\). Vậy \(\sin x < x\) với mọi \(x > 0\) Xét hàm số f(x) = x – sin x trên \(\left( { - \frac{\pi }{2};0} \right]\) Đạo hàm f’(x) = 1 - cos x > 0 \(\forall x \in \left( { - \frac{\pi }{2};0} \right)\) Do đó hàm số đồng biến trên \(\left( { - \frac{\pi }{2};0} \right]\) ⇒ f(x) < f(0) hay x- sin x < 0 \( \Leftrightarrow x < \sin x,\forall x \in \left( { - \frac{\pi }{2};0} \right]\) + Hiển nhiên: x < sin x với mọi \(x \le - \frac{\pi }{2}\) (vì \(x \le - \frac{\pi }{2} < - 1 \le \sin x\)) Do đó x < sin x với mọi x < 0. Cách giải thích khác: * Với mọi \(x<0\), áp dụng chứng minh ở trường hợp x > 0 ta có: \(\sin \left( { - x} \right) < - x \) (do x < 0 thì -x > 0) \(\Rightarrow - \sin x < - x \Rightarrow \sin x > x\) Vậy \(\sin x > x\) với mọi \(x<0\). LG b \(\cos x > 1 - {{{x^2}} \over 2}\) với mọi \(x \ne 0\) Lời giải chi tiết: Hàm số \(g\left( x \right) = \cos x + {{{x^2}} \over {2 }}-1\) liên tục trên \(\left[ {0; + \infty } \right)\) và có đạo hàm \(g'\left( x \right) = x - \sin x\) Theo câu a) \(g'\left( x \right) > 0\) với mọi \(x>0\) nên hàm số g đồng biến trên \(\left[ {0; + \infty } \right)\), khi đó ta có \(g\left( x \right) > g\left( 0 \right) = 0\) với mọi \(x>0\), tức là \(\cos x + {{{x^2}} \over 2} - 1 > 0\) với mọi \(x>0\) hay \(\cos x > 1 - {{{x^2}} \over 2}\) với mọi \(x>0\) (1) Với mọi x < 0 thì -x > 0 nên theo (1) ta có: \(\cos \left( { - x} \right) > 1 - {{{{\left( { - x} \right)}^2}} \over 2}\) \(\Leftrightarrow \cos x > 1 - \,{{{x^2}} \over 2}\) với mọi \(x < 0\)
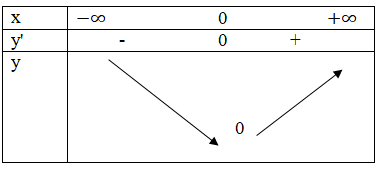
Vậy \(\cos x > 1 - \,{{{x^2}} \over 2}\) với mọi \(x \ne 0\). Cách khác: g’(x) = x – sin x g'(x)=0 \(\Leftrightarrow\) x- sin x = 0 ⇔ x = 0 Theo câu a ta có bảng biến thiên:
Từ bbt ta thấy \(g\left( x \right) > 0,\forall x \ne 0 \) \(\Leftrightarrow \cos x > 1 - \frac{{{x^2}}}{2},\forall x \ne 0\) LG c \(\sin x > x - {{{x^3}} \over 6}\) với mọi \(x > 0\); \(\sin x < x - {{{x^3}} \over 6}\) với mọi \(x<0\). Lời giải chi tiết: Hàm số \(h\left( x \right) = \sin x - x + {{{x^3}} \over 6}\) có đạo hàm \(h'(x) = \cos x - 1 + {{{x^2}} \over 2} > 0\) với mọi \(x \ne 0\) (câu b) Do đó \(h\) đồng biến trên \(\mathbb R\) nên ta có: \(h\left( x \right) > h\left( 0 \right) = 0,\forall x > 0\) và \(h\left( x \right) < h\left( 0 \right) = 0,\forall x < 0\) Từ đó suy ra: \(\sin x > x - {{{x^3}} \over 6}\) với mọi \(x>0\) \(\sin x < x - {{{x^3}} \over 6}\)với mọi \(x<0\) Loigiaihay.com
|




















Danh sách bình luận