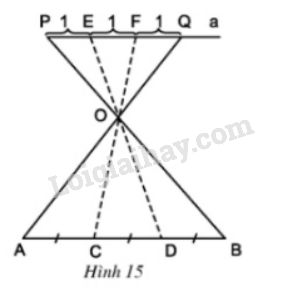
Bài 8 trang 63 SGK Toán 8 tập 2

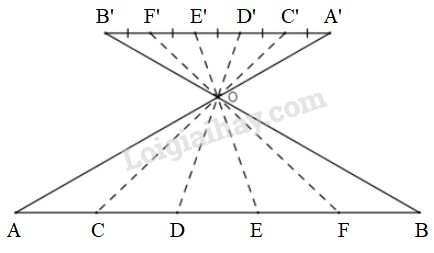
LG a.

Để chia đoạn thẳng AB thành ba đoạn bằng nhau, người ta đã làm như hình 15.

Hãy mô tả cách làm trên và giải thích vì sao các đoạn AC, CD, DB bằng nhau?

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet.

Lời giải chi tiết:

Mô tả cách làm:

Vẽ đoạn $PQ$ song song với $AB, PQ$ có độ dài bằng $3$ đơn vị

- Trên PQ lấy lần lượt các điểm E, F sao cho $PE=EF=FQ=1$ đơn vị 

- Xác định giao điểm $O$ của hai đoạn thẳng $PB$ và $QA$.

- Vẽ các đường thẳng $EO, FO$ cắt $AB$ tại $C$ và $D$.

Chứng minh $AC= CD = DB$

$∆OPE$ và $∆OBD$ có $PE//DB$ (theo cách vẽ) nên $\dfrac{DB}{PE} =  \dfrac{OD}{OE}$     (1) (hệ quả định lý TaLet)

$∆OEF$ và $∆ODC$ có $EF // CD$ (theo cách vẽ) nên $\dfrac{CD}{EF} = \dfrac{OD}{OE}=\dfrac{OC}{OF}$    (2) (hệ quả định lý TaLet)

$∆OFQ$ và $∆OCA$ có $FQ // AC$ (theo cách vẽ) nên $\dfrac{AC}{FQ} = \dfrac{OC}{OF}$    (3) (hệ quả định lý TaLet)

Từ (1), (2) và (3) suy ra:

$\dfrac{DB}{PE} = \dfrac{CD}{EF}=\dfrac{AC}{FQ}$ mà $PE = EF=FQ$ (gt) nên $DB = CD=AC$. 

Vây: $DB = CD = AC$.

LG b.

Bằng cách tương tự, hãy chia đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm trên mà vẫn có thể chia đoạn AB cho trước thành 5 đoạn bằng nhau?

Phương pháp giải:

Áp dụng: Hệ quả của định lý TaLet.

Lời giải chi tiết:

Tương tự chia đoạn thẳng $AB$ thành $5$ đoạn bằng nhau thực hiện như hình vẽ sau:

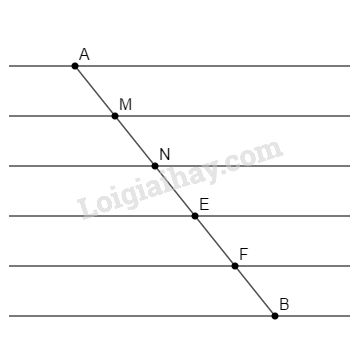
Cách khác: Ta có thể chia đoạn thẳng $AB$ thành $5$ đoạn thẳng bằng nhau như cách sau:

Vẽ $6$ đường thẳng song song cách đều nhau (có thể dùng thước kẻ để vẽ liên tiếp). Đặt đầu mút $A$ và $B$ ở hai đường thẳng ngoài cùng thì các đường thẳng song song cắt $AB$ chia thành $5$ phần bằng nhau. 

Loigiaihay.com